Here we consider a circular plate of radius a: it carries a load of intensity q uniformly distributed over its entire surface and the edges are clamped.
| Young’s modulus | E | 1,00E08 | kPa |
| Thickness | h | 1,00 | m |
| Poisson’s ratio | \(\nu\) | 0,30 | – |
| Radious | a | 10,00 | m |
| Uniform pressure | q | -10,00 | kPa |
| Flexural rigidity of the plate | D | 9157509,16 | kN/m |
The flexural rigidity of the plate is \(D = {E \cdot h^3}/{12(1-\nu^2)}\).
If you want, you can read how we built the model in WeStatiX in our documentation. In here you find also dimensions and material constants. Otherwise, you can find it amongst our tutorials.
The analytical solution of this problem is given in Theory of plates and shells, [1].
If \(D= \frac{E h^3}{12 (1-\nu^2)}\) is the stiffness of the plate, we expect the deflection to be \(w(x)= \frac{q}{64D} (a^2-r^2)^2\)
While the bending moments are:
\(M_r= \frac{q}{16} [a^2(1+\nu)-r^2 (3+\nu); \) is the bending moment acting along circumferential sections of the plate.
\(M_t= \frac{q}{16} [a^2(1+\nu)-r^2 (1+3\nu)\) is the bending moment acting along the diametral sections of the plate.
Start the analysis in the CALCULATE Tab, so you can read the results contours as in the pictures below.
Remember that they refers to the global axes.
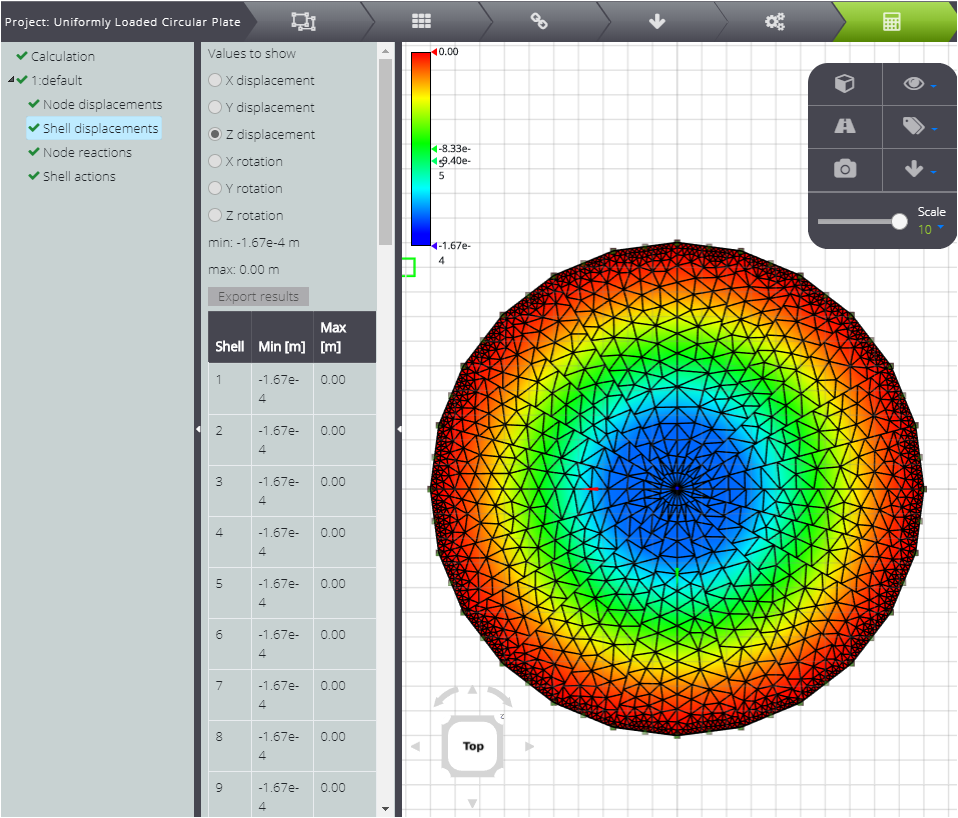

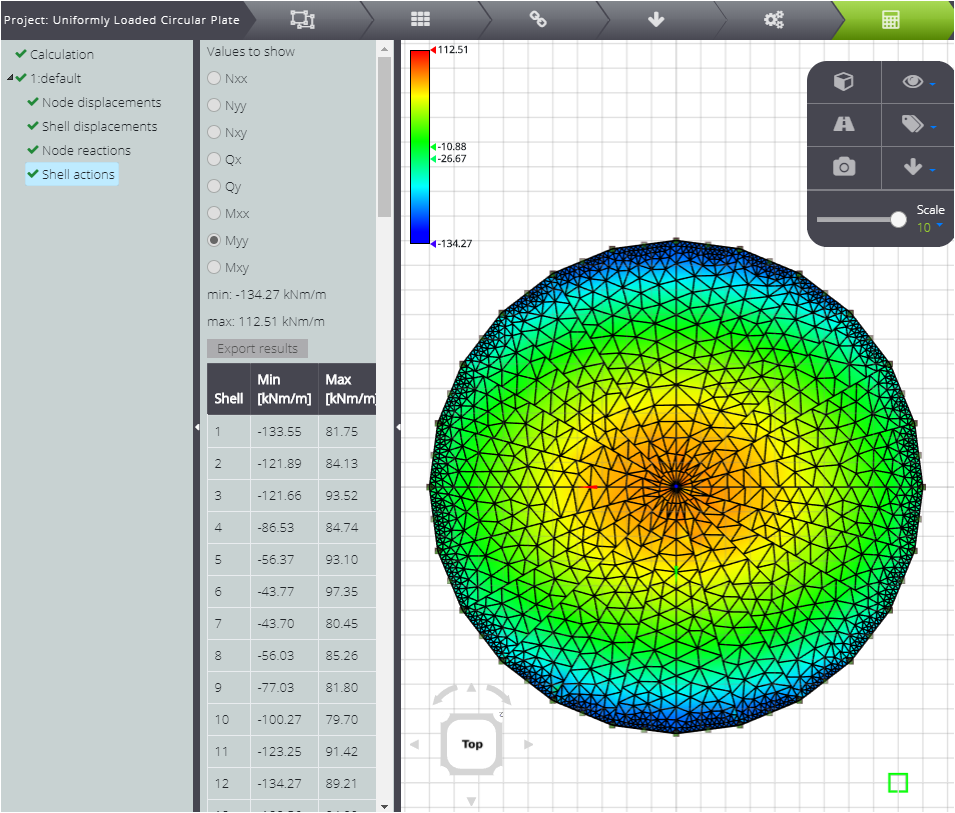
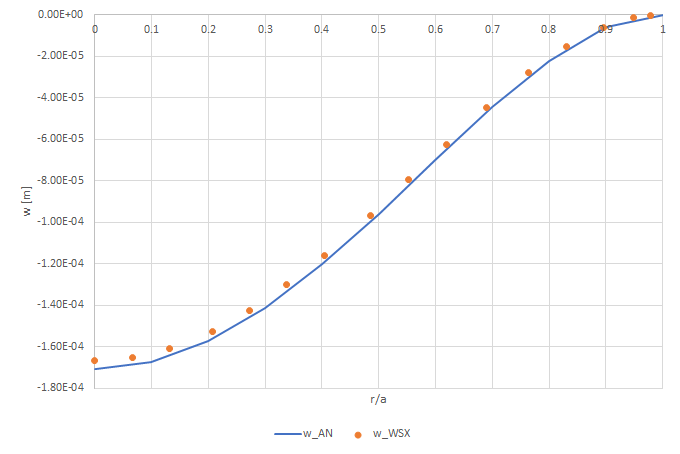
In order to compare the numerical solution with the analytical one, you can export the results and plot them. Therefore you can see the comparison between the two solutions.
First, the displacements.
Secondly, the bending moment \(M_r\).
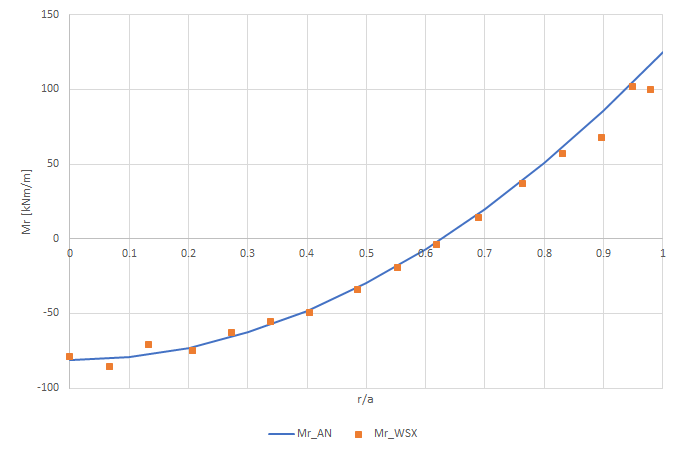
In the end, the bending moment \(M_t\)
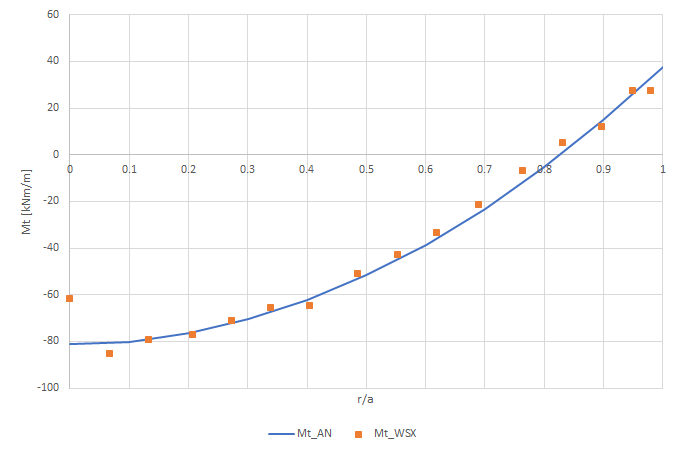
[1] TIMOSHENKO S., WOINOWSKY Y-RIEGER S., Theory of plates and shells, 2ed., McGraw-Hill, New York, 1959
