In this example a cantilever beam is subjected to a constant load: the results are determined entirely online and compared with the well-known analytical solution.
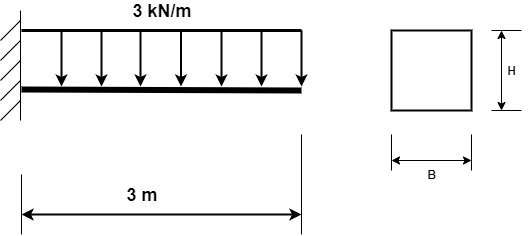
\(E = 210 GPa\)
\(B = H = 0.1 m\)
Build the model using the data shown in the figure above! In our tutorial we explain how to do it on a similar model, otherwise you can find it ready for the calculation in WeStatiX, so you can go directly to the Tab CALCULATE and run the analysis.
We are ready to compare the numerical solution with the analytical one.
The analytical solution for deflection is:
\(v(x)= \frac{q_0}{24EI}x^2 (x^2-4Lx +6L^2)\)
You can easily obtain it by calculating the static beam equation with proper boundary conditions modelling supports.
So now you can get:
- the deflection at the tip as \(f = v(L) \frac{q l^4}{8EJ}\)
- the rotation at the tip as \(\phi = \frac{q l^3}{6EJ} \)
- the vertical reaction forceas \(V = ql \)
- the reaction moment can as \(M = \frac{ql^2}{2} \)
Result Comparison
| Result Type | Target Value | WeStatiX result | RElative Error |
|---|---|---|---|
| Deflection at free end [m] | 0.017357 | 0.017357 | 0,00% |
| Rotation at free end [rad] | 0.007714 | 0.007714 | 0,00% |
| Vertical reaction force [kN] | 9 | 9 | 0,00% |
| Reaction moment [kNm] | 13.5 | 13.5 | 0,00% |
WeStatiX captures the analytical solution perfectly.
