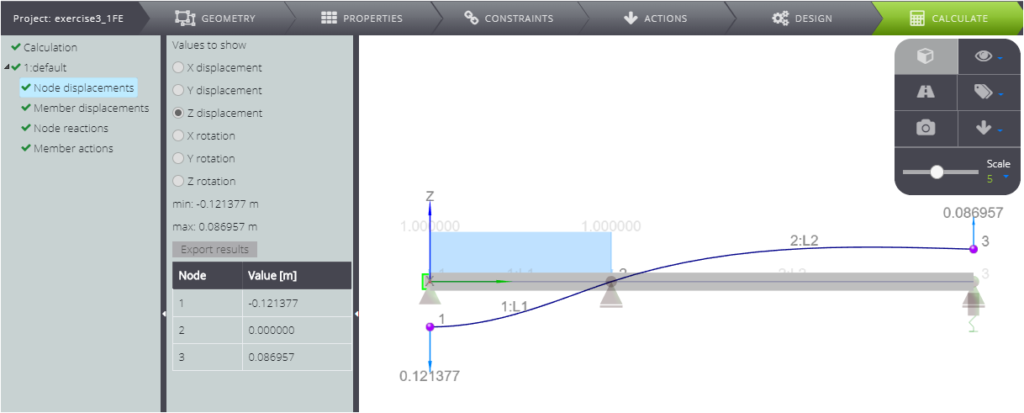
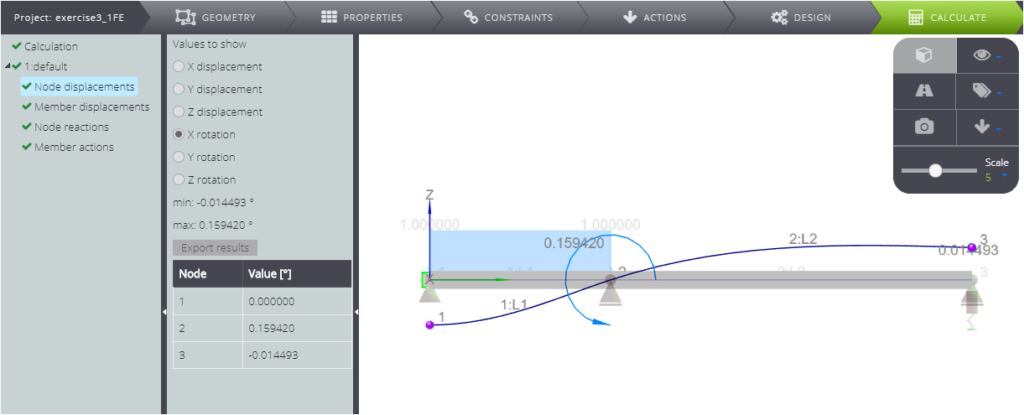
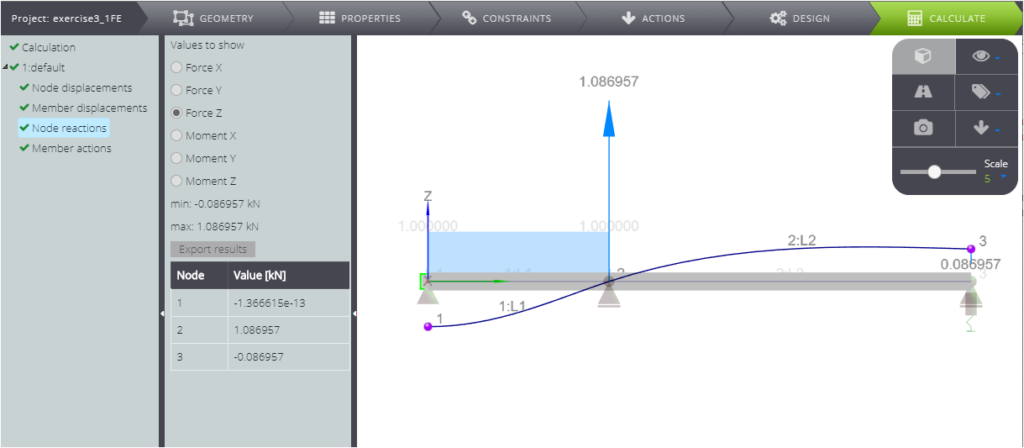
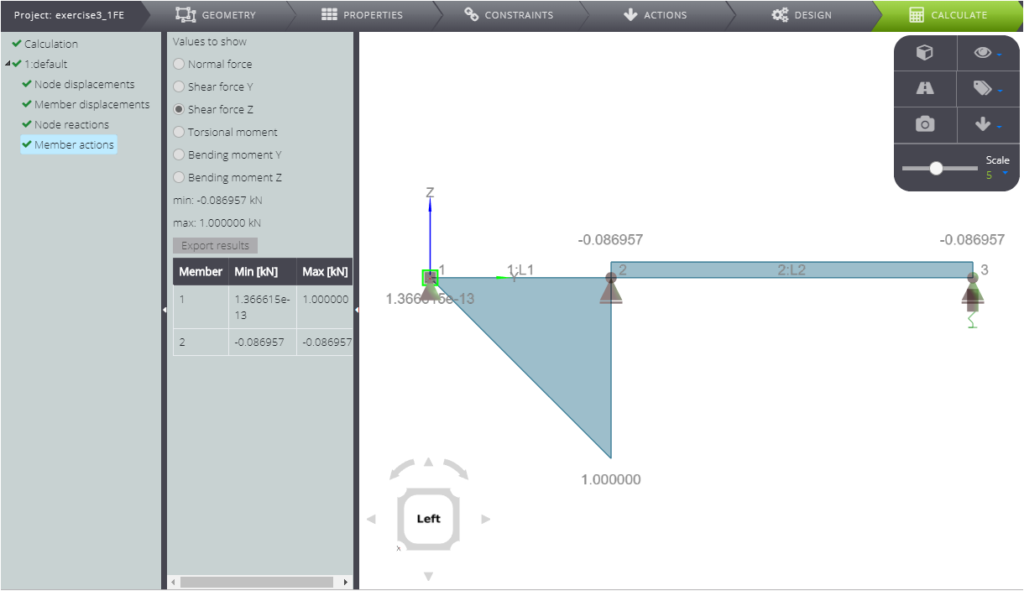
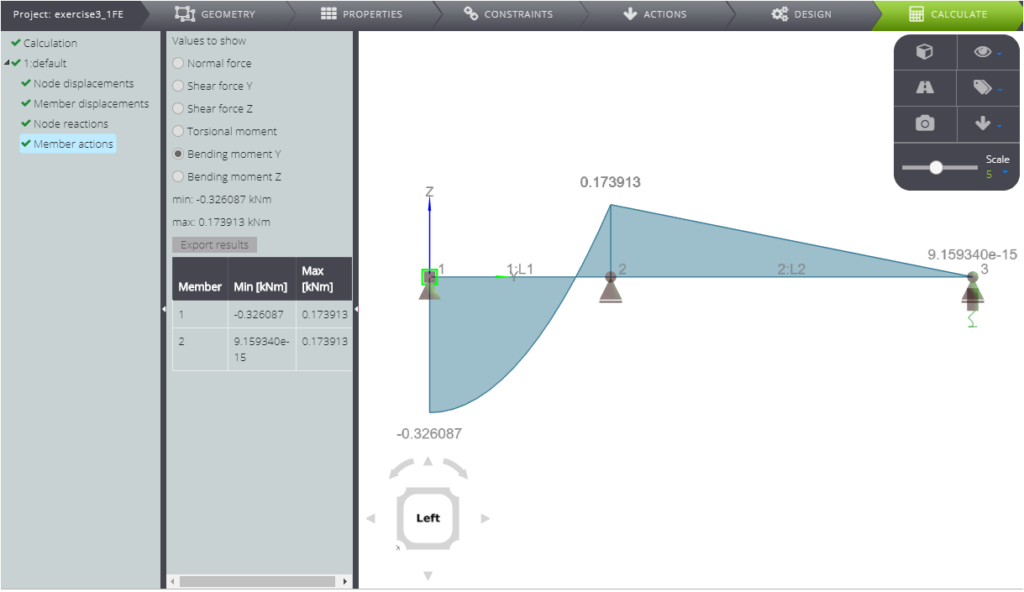
In this section we want to show you the comparison between the analytical solution and the numerical one for the system below.
| Young’s modulus | E | 1,00 | kPa |
| Section | A | 0,01 | \(m^2\) |
| Length | L | 1,00 | m |
| Moment of inertia | J | 1,00 | \(m^4\) |
| Load | q | -1,00 | \(kN/m\) |
You can learn how to build the model in WeStatiX or just run the calculation, it’s already in our tutorials!
As usually you can find the beam equation modelling supports and loads as boundary conditions.
After that you get these two equation for the deflection
The first one is valid \( 0<x<L\)
\(v_{AN1} (x) = \frac{q (67L^4 – 90L^2 x^2 + 23 x^4)}{552EI}\)
The second one between \( L<x<3L\)
Consequently you can find the expressions for rotation, bending moment and shear forces.
In the table below we confront the value of various parameters with the WeStatiX’s solution.
| Description | Parameter | UM | Analytical solution | Analytical solution | WSX | Error |
|---|---|---|---|---|---|---|
| Vertical displacement in A | \(v_{A}\) | m | \(67 qL^4/ 552 EJ\) | -0,12138 | -0,12138 | 0,00% |
| Rotation in B | \(\phi_B\) | rad | \(11 qL^3/ 69 EJ\) | 0,15942 | 0,15942 | 0,00% |
| Rotation in C | \(\phi_C\) | rad | \(qL^3/ 69 EJ\) | -0,01449 | -0,01449 | 0,00% |
| Bending moment in A | \(M_A\) | kNm | \(15 qL^2/46\) | -0,32609 | -0,32609 | 0,00% |
| Bending moment in B | \(M_B\) | kNm | \(4 qL^2/23\) | 0,17391 | 0,17391 | 0,00% |
| Bending Moment in C | \(M_C\) | kNm | \(0\) | 0,00000 | 0,00000 | 0,00% |
| Shear force in A | \(T_A\) | kN | \(0\) | 0,00000 | 0,00000 | 0,00% |
| Shear force in B | \(T_B\) | kN | \(qL\) | 1,00000 | 1,00000 | 0,00% |
| Shear force in C | \(T_C\) | kN | \(2qL/23\) | -0,08696 | -0,08696 | 0,00% |
Finaly in the figure you can read all the results.