Consider a uniformly loaded and simply supported square plate: the problem’s data are listed in the table below.
| Young’s modulus | E | 100.000.000 | kPa |
| Thickness | h | 0,30 | m |
| Poisson’s ratio | \(\nu\) | 0,30 | – |
| Length | a | 10,00 | m |
| Uniform pressure | q | -10,00 | kPa |
| Flexural rigidity of the plate | D | 247252,75 | kN/m |
The flexural rigidity is calculated as \( {E \cdot h^3}/{12(1-\nu^2)}\)
You can find the model in our tutorials in WeStatiX. Alternatively you can build it yourself: you can read how to do it in our documentation.
Once geometry, properties and boundary conditions are defined, you just have to start the analysis to get the results.
This is the displacements’ field.
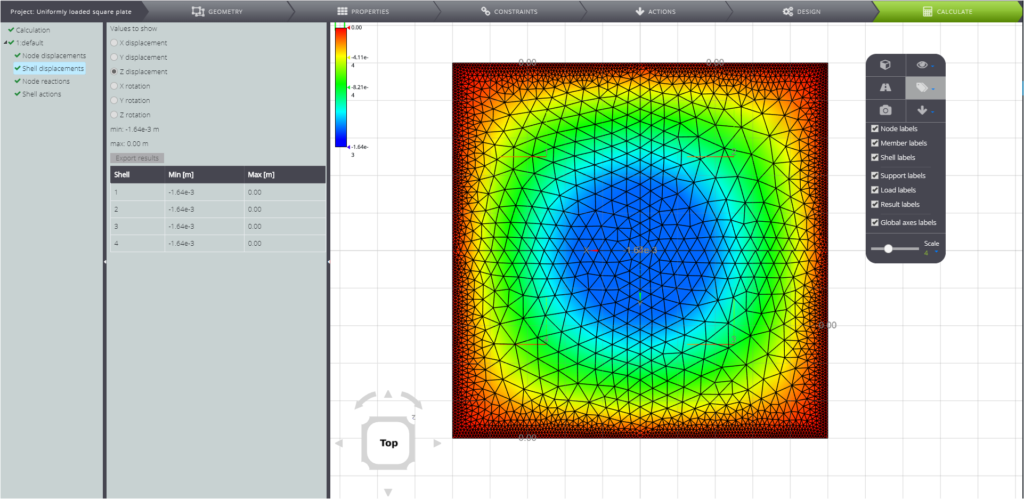
Secondly, the bending moment
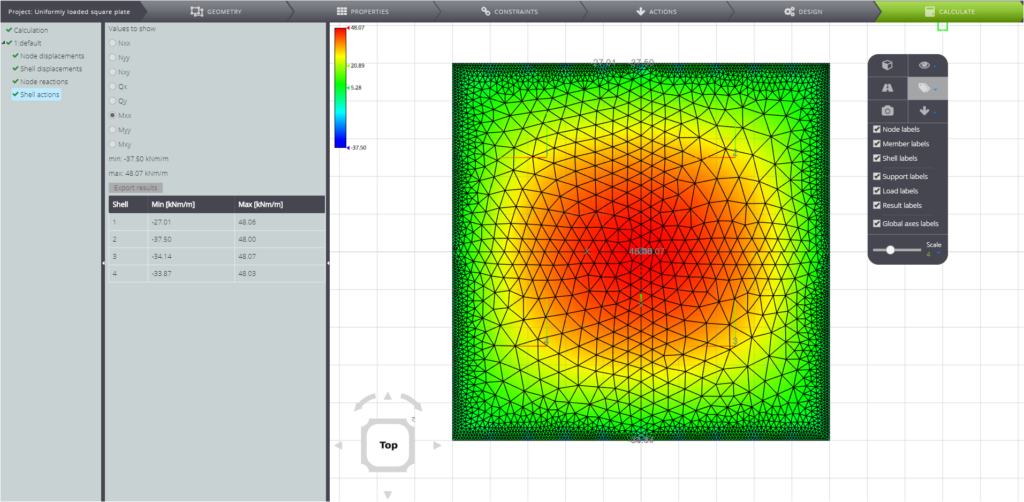
And finally, the nodal forces.
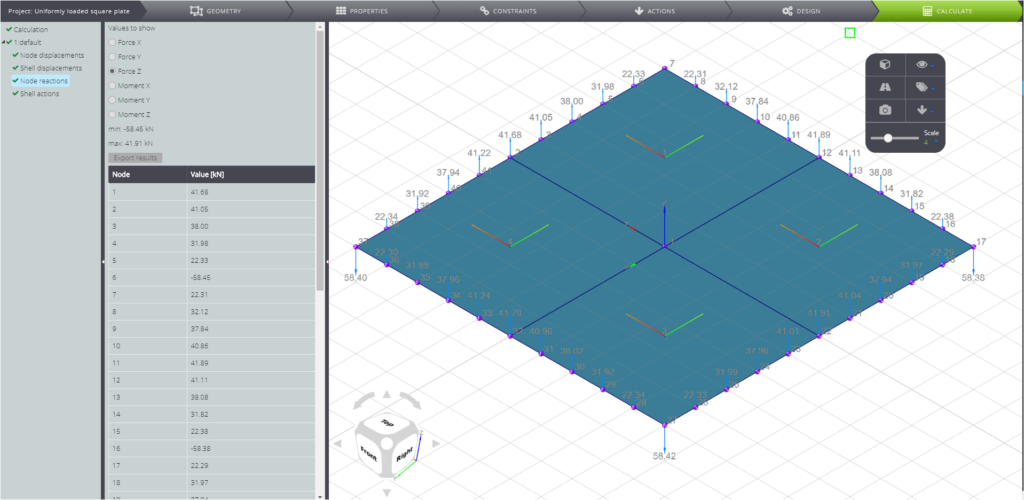
Please note that the corners of the plate have a tendency to rise up under the actions of the applied load. The concentrated forces R exist to prevent this and they are therefore directed downward. In order to catch the exact value of these forces you will need to make a finer mesh.
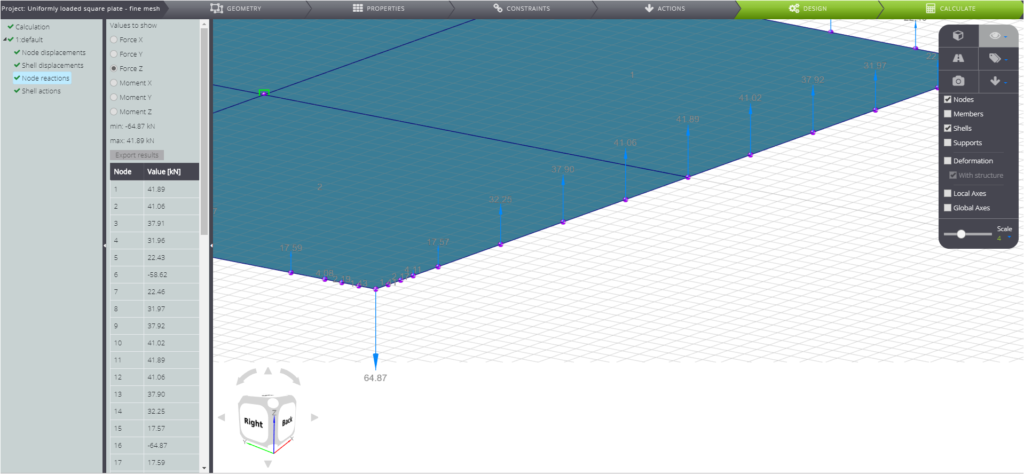
The analytical solution to the problem is known, and you can find it in Theory of plates and shells [1] .
Below we compare the foundamental points of the solution with the results we obtained with our FE analysis.
| Description | Parameter | UM | Analytical solution | WSX – rough mesh | Error- rough mesh |
|---|---|---|---|---|---|
| Deflection | \(w_{max}\) | m | -0.016E-04 | -1,643E-03 | 0,04% |
| Bending moment | \(M_{x_{max}}\) | kNm/m | -47,90 | -48.07 | 0,35% |
| Reactive forces at the corners | R | kN | 65,00 | 58,45 | 11,21% |
And finally the comparison with the results obteined with the finest mesh.
| Description | Parameter | UM | Analytical solution | WSX – fine mesh | Error – fine mesh |
|---|---|---|---|---|---|
| Deflection | \(w_{max}\) | m | -0.016E-04 | -0.016E-04 | 0,04% |
| Bending moment | \(M_{x_{max}}\) | kNm/m | -47,90 | -47,91 | 0,02% |
| Reactive forces at the corners | R | kN | 65,00 | 64,87 | 0,20% |
[1] TIMOSHENKO S., WOINOWSKY Y-RIEGER S., Theory of plates and shells, 2ed., McGraw-Hill, New York, 1959.
