Do you need to design a reinforced concrete element under biaxial bending? In this example you can see how we validate WeStatiX’s accuracy in the calculation of the reinforcement cross-sectional area for a beam subjected to biaxial bending.
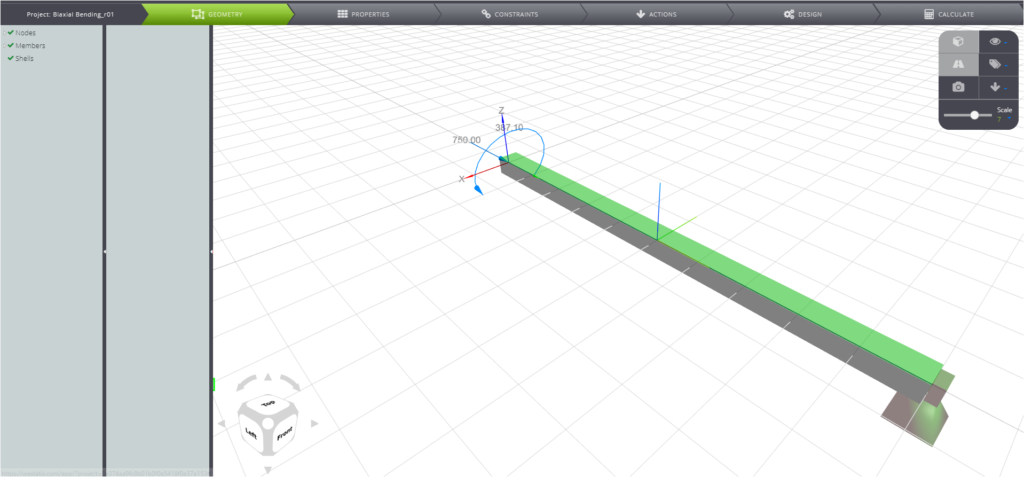
In WeStatiX you can find the model we utilized for this verification: it’s a cantilever beam subjected to biaxial bending and compressive axial force on its free end.
| Axial force | \(N_{Ed}\) | \(\) | 750 | kN |
| Bending moment X | \(M_{Ed,X}\) | \(\) | 225 | kNm |
| Bending moment Z | \(M_{Ed,Z}\) | \(\) | 315 | kNm |
The characteristics of the cross section are listed below.
| Description | Symbol | Value | UM | |
|---|---|---|---|---|
| Overall width of a cross-section | \(b\) | \(\) | 500 | mm |
| Height | \(h\) | \(\) | 400 | mm |
| concrete cover | \(d_1\) | \(\) | 70 | mm |
| concrete cover | \(d_2\) | \(\) | 70 | mm |
| \(d’\) | \(h-d_1\) | 330 | mm | |
| – | \(b’\) | \(b-d_2\) | 430 | mm |
| ratio for interaction diagram choice | \(d’/h\) | \(\) | 0,18 | – |
And finally, the material parameters
| Description | Symbol | value | UM | |
|---|---|---|---|---|
| Characteristic compressive cylinder strength of concrete at 28 days | \(f_{ck}\) | \(\) | 25.000,00 | kPa |
| Characteristic yield strength of reinforcement | \(f_{yk}\) | \(\) | 550.000,00 | kPa |
| Coefficient taking account of long term effects | \(\alpha_{cc}\) | \(\) | 1,00 | – |
| Partial factor for concrete | \(\gamma_c\) | \(\) | 1,50 | – |
| Partial factor for reinforcing steel | \(\gamma_s\) | \(\) | 1,15 | – |
| Design value of concrete compressive strength | \(f_{cd}\) | \(\alpha_{cc} f_{ck}/\gamma_c\) | 16.666,67 | kPa |
| Design value for yield strength of reinforcement | \(f_{yd}\) | \(f_{yk}/\gamma_{s}\) | 478.260,87 | kPa |
When the model is ready, you can start the analysis, and you will obtain the following diagrams.
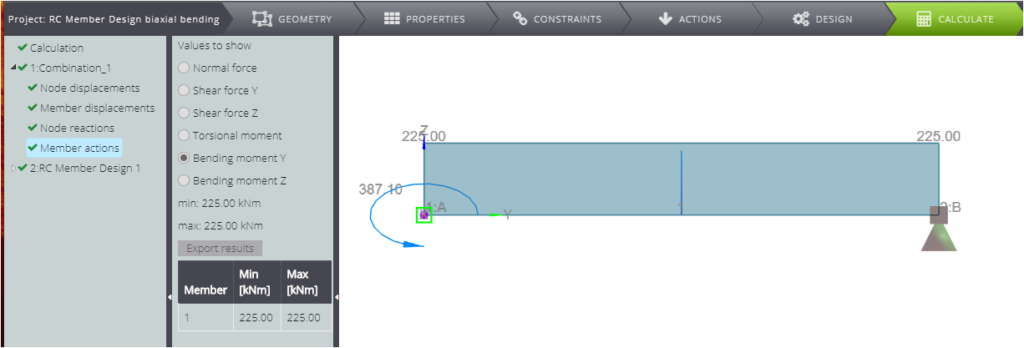
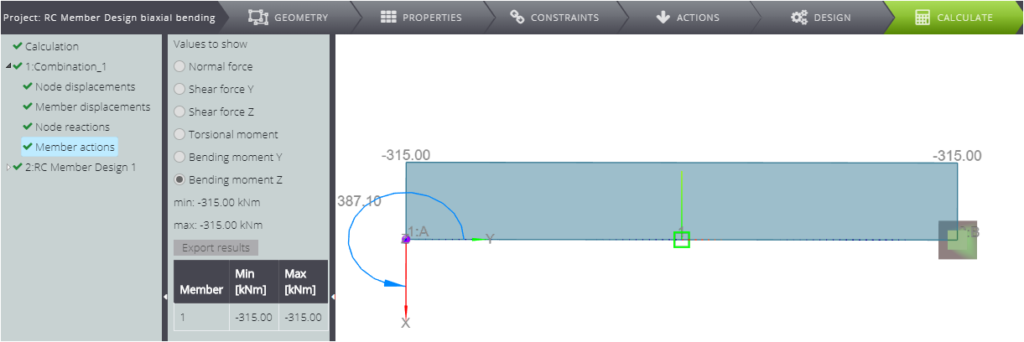
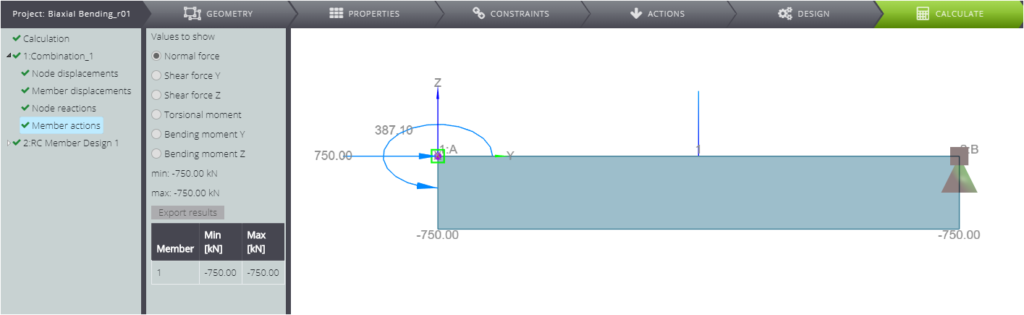
Focusing on the RC member design results, you can see that the total reinforcement area in the cross section is \(A_{s,tot}=46,17cm^2\).
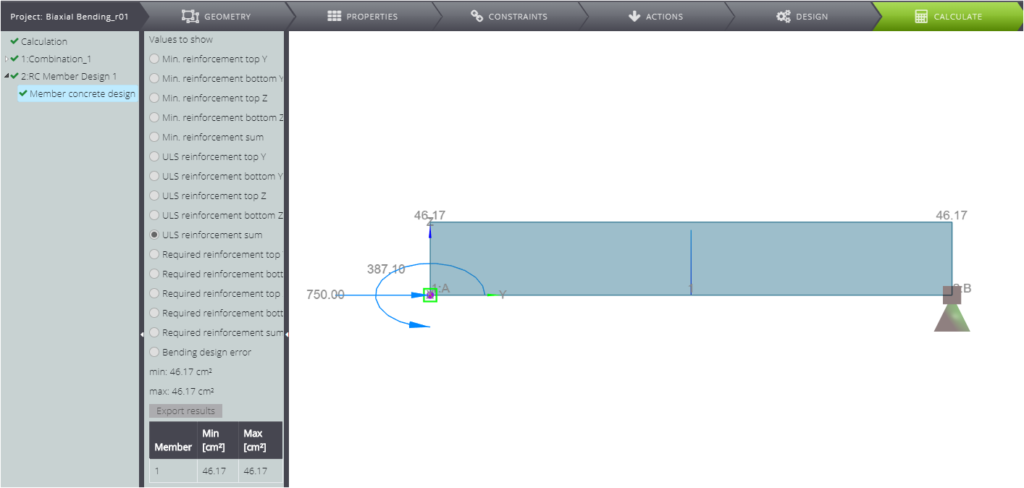
You can verify it with briefly with the interaction diagrams for the reinforced concrete design of a cross-section under biaxial bending. [1]
| Parameterized axial force | \(\nu\) | \(N_d/b \cdot h \cdot f_{cd}\) | 0,225 | – |
| \(\beta\) | \(0,6+\nu\) | 0,825 | – | |
| Fictitious eccentricity | \(e’_y\) | \(e_y + \beta \cdot e_z \cdot b / h\) | 0,733 | m |
| Effective uniaxial moment | \(M’_z\) | \(N_{Ed}\cdot e’_y\) | 549,84 | kNm |
| Parameterized bending moment | \(\mu\) | \(M’_z/b\cdot h^2 \cdot f_{cd}\) | 0,33 | – |
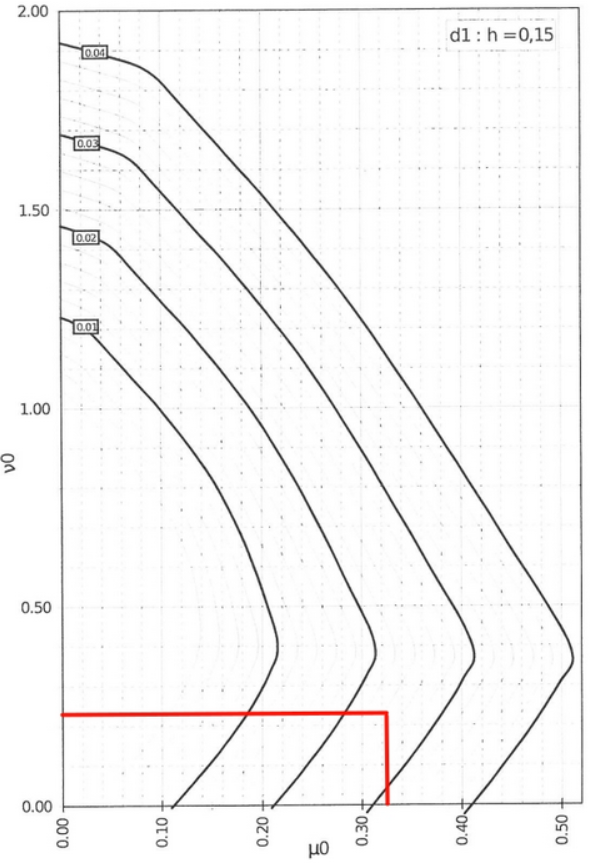
| Coefficient from interaction diagram | \(A_s / b \cdot h\) | \(\) | 0,02 | – |
| Total reinforcement area | \(A_{s,tot}\) | \(\) | 48,00 | cm^2 |
So the error is
\( \epsilon = 1-\frac{46,17}{48,00} = 3,81\% \)Which is acceptable since the interaction diagram method is approximate. WeStatiX’s solution is therefore verified.
[1] Scriptum zur Vorlesung BETONBAU 1 nach EC 1992-1-1, Technische Universität Wien, Institut für Tragkonstruktionen – Herausgegeben von Prof. Dr.-Ing. Johann KOLLEGER
