In this page we test the accuracy of WeStatiX solving the structure made of two cantilever beams connected by a truss. Data about geometry and material properties are listed in the table below.
| Young’s modulus | E | 1,00 | kPa |
| Length | H | 0,50 | m |
| Length | L | 1,00 | m |
| Moment of inertia | J | 1,00E00 | \(m^4\) |
| Distributed Load | q | -1,00 | \(kN/m\) |
| Point load | P | -1,00 | \(kN\) |
You can easily build the model in WeStatiX as we show in our tutorial, or you can find it already done in our public projects.
You can of course solve the beam equation in order to obtain the analytical results.
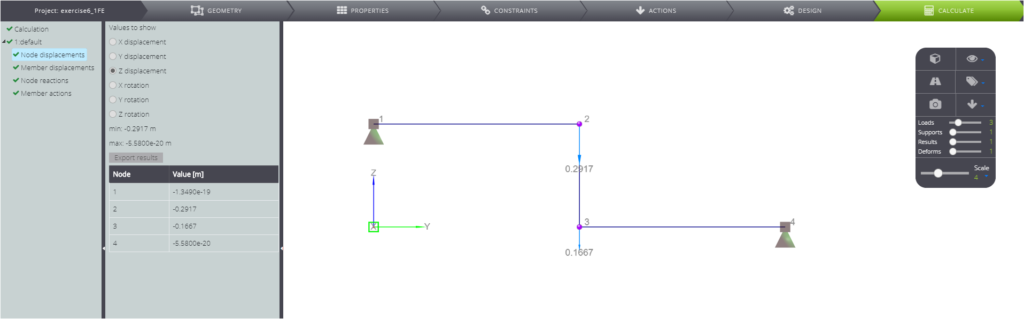
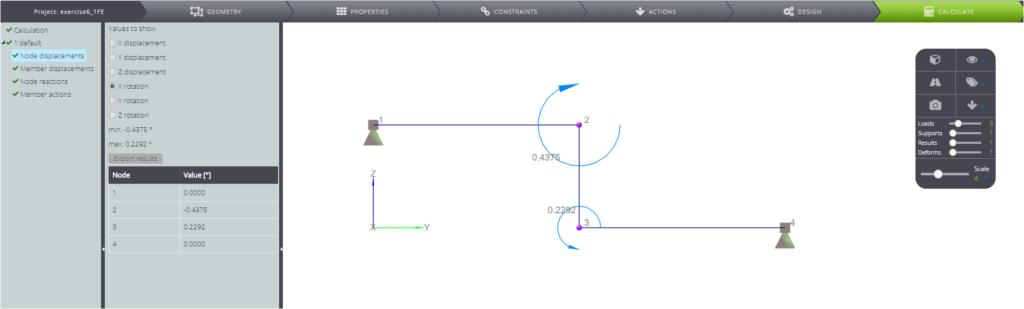
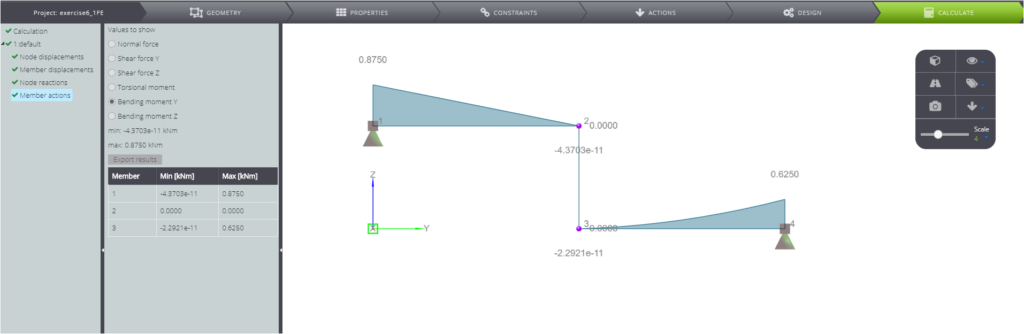
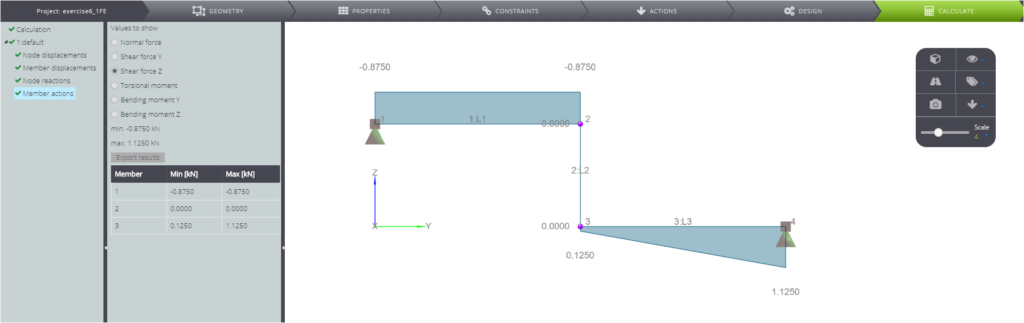
In the following table the main points of the solution are displayed and compared with WeStatiX’s results.
| Description | Parameter | UM | Analytical solution | Analytical solution | WSX | Error |
|---|---|---|---|---|---|---|
| Vertical displacement in B | \(v_{B}\) | m | \(7qL^4/24EJ\) | -0,29167 | -0,29170 | 0,01% |
| Rotation in B | \(\phi_B\) | rad | \(7qL^3/16EJ\) | -0,43750 | -0,43750 | 0,00% |
| Vertical displacement in C (right) | \(v_C\) | m | \(1qL^4/6EJ\) | -0,16667 | -0,16670 | 0,02% |
| Rotation in C | \(\phi_C\) | rad | \(11qL^3/48EJ\) | 0,22917 | 0,22920 | 0,01% |
| Bending moment in A | \(M_A\) | kNm | \(7qL^2/8\) | 0,87500 | 0,87500 | 0,00% |
| Bending moment in D | \(M_D\) | kNm | \(5qL^2/8\) | 0,62500 | 0,62500 | 0,00% |
| Shear force in A | \(T_A\) | kN | \(7qL/8\) | -0,87500 | -0,87500 | 0,00% |
| Shear force in B (right) | \(T_B^{r}\) | kN | \(1qL/8\) | 0,12500 | 0,12500 | 0,00% |
| Shear force in C | \(T_C\) | kN | \(9qL/8\) | 1,12500 | 1,12500 | 0,00% |
| Normal force in B | \(T_B^{r}\) | kN | \(1qL/8\) | -0,12500 | -0,12500 | 0,00% |
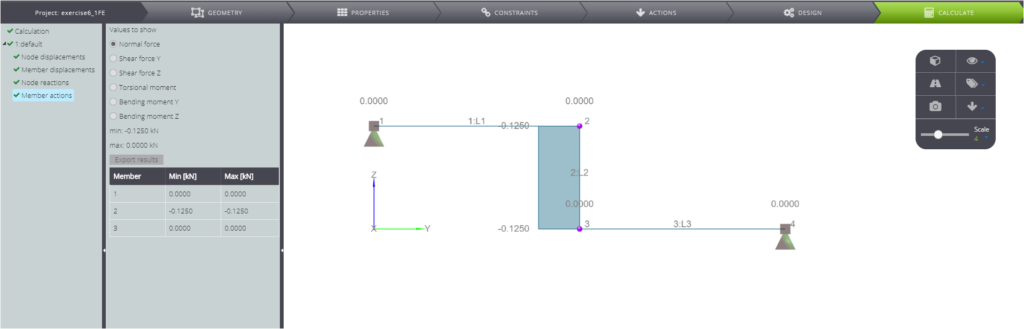
Finally, in the following pictures you can see the calculated results.