In this page we compare the analytical and the numerical solution for an uniformly loaded square plate supported at the corners.
You can read the data in the table below.
| Young’s modulus | E | 100.000.000 | kPa |
| Thickness | h | 0,30 | m |
| Poisson’s ratio | \(\nu\) | 0,30 | – |
| Length | a | 10,00 | m |
| Uniform pressure | q | -10,00 | kPa |
| Flexural rigidity of the plate | D | 247253,75 | kN/m |
The flexural rigidity of the plate is computed as \( {E \cdot h^3}/{12(1-\nu^2)}\).
If you need to understand how to build the model, you can read in our documentation how we built a similar one. You just have to follow the steps except for the supports on the nodes along the edges.
Otherwise you can find it through our public tutorials in WeStatiX, you just need to start the calculation.
Now you can compare the results with the solution given in Theory of plates and shells [1].
| Description | Parameter | UM | Analytical solution | WSX | Error |
|---|---|---|---|---|---|
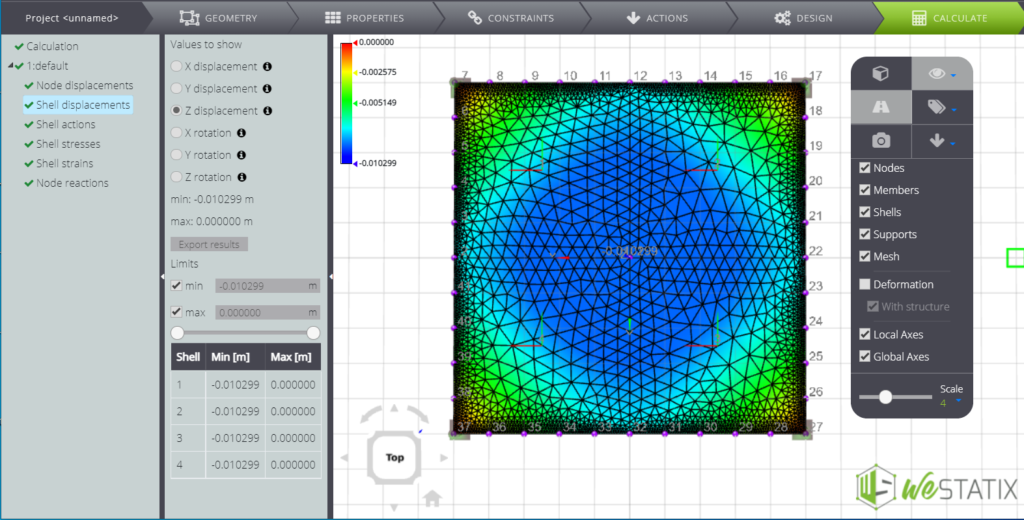
| Deflections (x=0; y=0) | \(w_{max}\) | m | -1,01E-02 | -1,03E-02 | 2% |
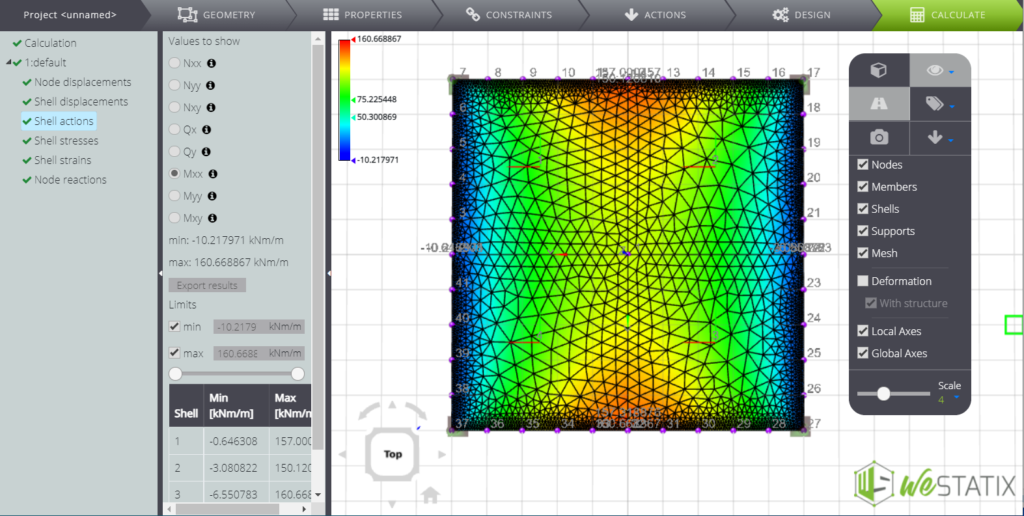
| Bending moment in the centre of the plate (x=0; y=0) | \(M_{x _{max}}\) | kNm/m | -109,00 | -108,594 | 0% |
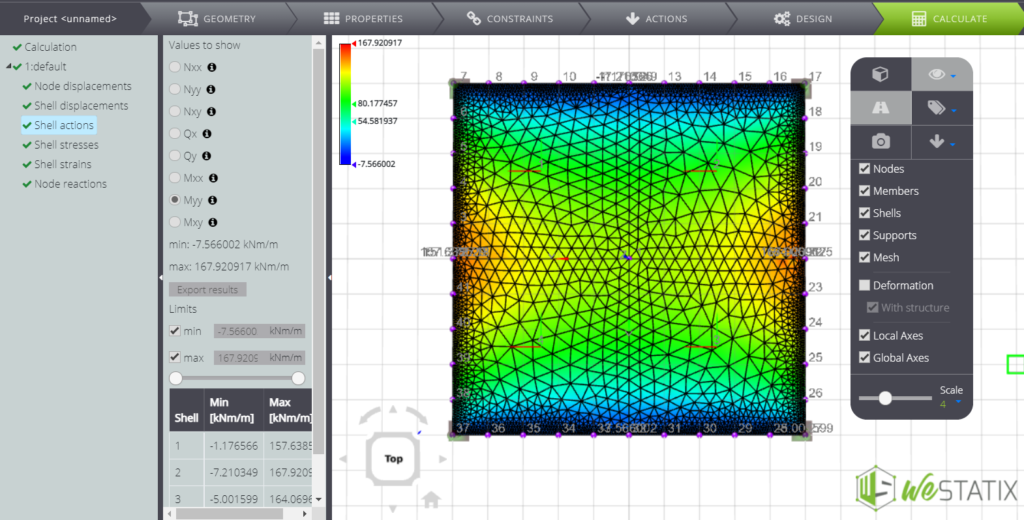
| Bending moment on the edge (x=0; y=a/2) | \(M_{y _{max}}\) | kNm/m | -140,40 | -142,716 | 2% |
Finally, we here you can see some screenshots of the results.
[1] TIMOSHENKO S., WOINOWSKY Y-RIEGER S., Theory of plates and shells, 2ed., McGraw-Hill, New York, 1959.
