Beam subjected to uniform temperature rise

In this page we consider a one-dimensional beam fixed at both ends subjected to an uniform temperature rise T.

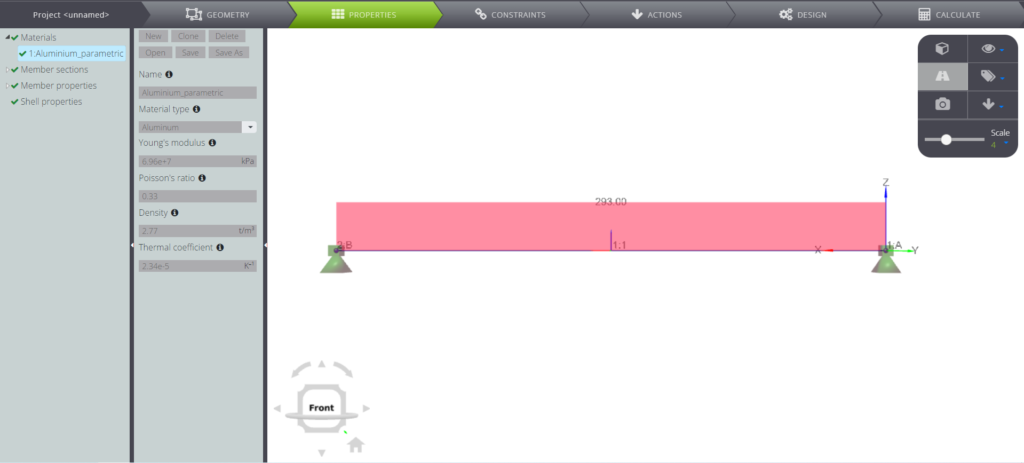
If you want, you can build the FE model with the data shown in the following table.

Young’s modulus	E	69637000	kPa
Section	A	1,00	\(m^2\)
Length	L	10,00	m
Coefficient of thermal expansion	\(\alpha\)	0,0000234	1/K
Temperature increase	T	293,00	K

On the other hand, you can find it through our tutorials, so you just have to start the calculation.

First you have to determine the analytical solution: in order to do it, consider the axial direction. [1] The strain on the beam due to uniform temperature change is:

\(\epsilon_T=\alpha \cdot T\)

The stress/strain law is linear, therefore the nodal forces must be

\(F=A \cdot \sigma=A \cdot E \cdot \epsilon = A \cdot E \cdot \alpha \cdot T\)

Therefore you can compare the analytical solution with WeStatiX’s results, as shown in the following table.

Description	Parameter	UM		Analytical solution	WSX	Error
Force	\(F\)	kN		477445	477445	0,00%

In the pictures you can see the diagram of the normal force.

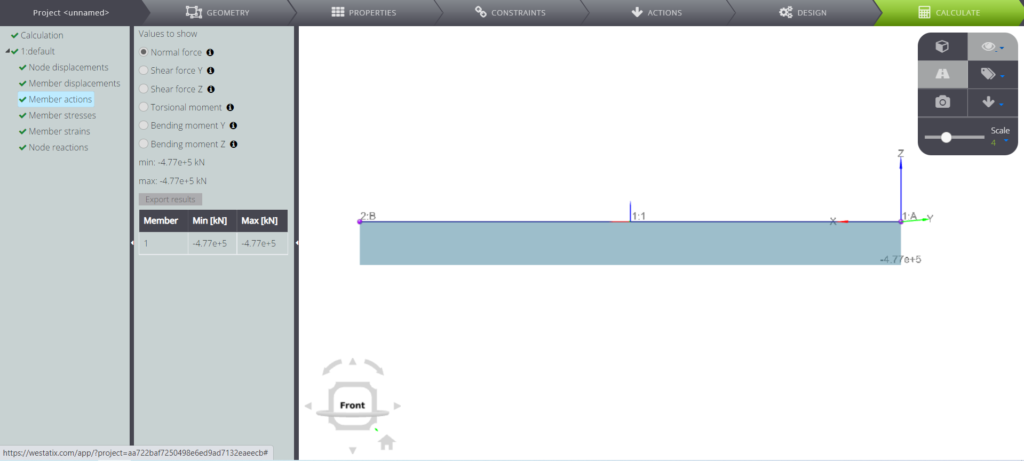
WeStatiX catches the solution perfectly.

[1] DARYL L. LOGAN, A First Course in the Finite Element Method, 4th edition, Thomson