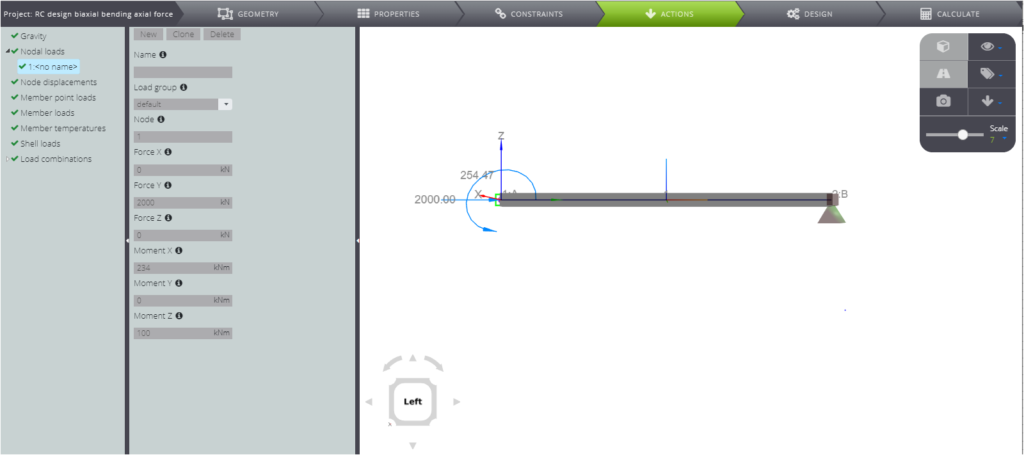
In this page we discuss the results for RC design for a cantilever beam subjected to biaxial bending and axial force.
| Axial force | \(N_{Ed}\) | \(\) | 2000 | kN |
| Bending moment X | \(M_{Ed,X}\) | \(\) | 234 | kNm |
| Bending moment Z | \(M_{Ed,Z}\) | \(\) | 100 | kNm |
You can find the model in WeStatiX ready for your calculation.
In the table below you can read the cross section parameters
| Description | Symbol | Value | UM | |
|---|---|---|---|---|
| Overall width of a cross-section | \(b\) | \(\) | 300 | mm |
| Height | \(h\) | \(\) | 400 | mm |
| Top concrete cover | \(d_1\) | \(\) | 50 | mm |
| Bottom concrete cover | \(d_2\) | \(\) | 50 | mm |
| \(d’\) | \(h-d_1\) | 350 | mm | |
| – | \(b’\) | \(b-d_2\) | 250 | mm |
| ratio for interaction diagram choice | \(d’/h\) | \(\) | ,13 | – |
And the material parameters
| Description | Symbol | value | UM | |
|---|---|---|---|---|
| Characteristic compressive cylinder strength of concrete at 28 days | \(f_{ck}\) | \(\) | 42.500,00 | kPa |
| Characteristic yield strength of reinforcement | \(f_{yk}\) | \(\) | 549.700,00 | kPa |
| Coefficient taking account of long term effects | \(\alpha_{cc}\) | \(\) | 1,00 | – |
| Partial factor for concrete | \(\gamma_c\) | \(\) | 1,50 | – |
| Partial factor for reinforcing or prestressing steel | \(\gamma_s\) | \(\) | 1,15 | – |
| Design value of concrete compressive strength | \(f_{cd}\) | \(\alpha_{cc} f_{ck}/\gamma_c\) | 28.333,33 | kPa |
| Design value for yield strength of reinforcement | \(f_{yd}\) | \(f_{yk}/\gamma_{s}\) | 478.000,00 | kPa |
If you take a look to the RC member design results you will find the total area of reinforcement to be \(A_{s,tot}=29,02 cm^2\).
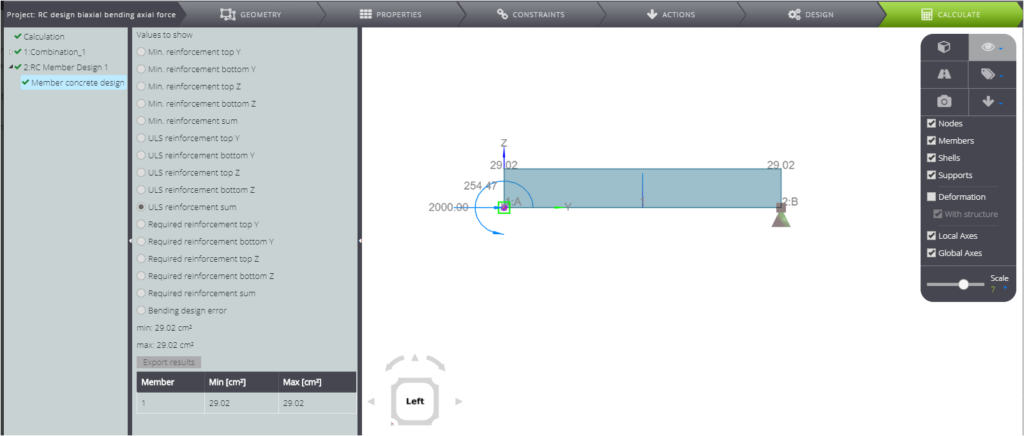
You can check it by using the interaction diagrams as suggested in [1]. According to it, you need to find the following parameters
| \(\beta\) | \(1-N_d/b \cdot h \cdot f_{ck}\) | 0,61 | – | |
| Effective uniaxial moment | \(M’_z\) | \(M_x+\beta M_y d/b’ \) | 322,64 | kNm |
| Parameterized axial force | \(\nu\) | \(N_d/b \cdot h \cdot f_{cd}\) | 0,59 | – |
| Parameterized bending moment | \(\mu\) | \(M’_z/b\cdot h^2 \cdot f_{cd}\) | 0,24 | – |
So you have to consider the interaction diagrams for the design for biaxial bending and axial force for a section with d’/h=0,10 and d’/h=0,15, showed below

It’s easy then to find the reinforcement total area
| Coefficient from interaction diagram | \(A_s \cdot f_{yd} / b \cdot h \cdot f_{cd}\) | \(\) | 0,41 | – |
| Total reinforcement area | \(A_{s,tot}\) | \(\) | 29,16 | cm^2 |
You can finally calculate the error as follows
WeStatiX matches the solution.
[1] A.W.. BEEBY and R.S: NARAYANAN – Designers’ guide to Eurocode 2: design of concrete structures. – Designers’ guide to EN1992-1-1 and EN1992-1-2 Eurocode 2: design of concrete structures. General rules and rules for buildings and structural fire design.
