In questa pagina consideriamo una trave unidimensionale fissata ad entrambe le estremità e sottoposta ad un aumento uniforme della temperatura T.
È possibile costruire il modello FE con i dati riportati nella seguente tabella.
| Modulo di Young | E | 69637000 | kPa |
| Sezione | A | 1,00 | \(m^2\) |
| Lunghezza | L | 10,00 | m |
| Coefficiente di dilatazione termica | \(\alpha\) | 0,0000234 | 1/K |
| Aumento della temperatura | T | 293,00 | K |
D’altra parte, è possibile trovarlo anche nei nostri tutorial, quindi non resta che iniziare il calcolo.
Per prima cosa bisogna determinare la soluzione analitica: per farlo, occorre considerare la direzione assiale. [1] La deformazione della trave dovuta alla variazione uniforme della temperatura è:
\(\epsilon_T=\alpha \cdot T\)
La legge stress/deformazione è lineare, quindi le forze nodali devono essere
Pertanto è possibile confrontare la soluzione analitica con i risultati di WeStatiX, come mostrato nella seguente tabella.
| DESCRIZIONE | PARAMETRO | UM | SOLUZIONE ANALITICA | WSX | ERRORE | |
|---|---|---|---|---|---|---|
| Forza | \(F\) | kN | 477445 | 477445 | 0,00% |
Nelle immagini è mostrato il diagramma dello sforzo normale.
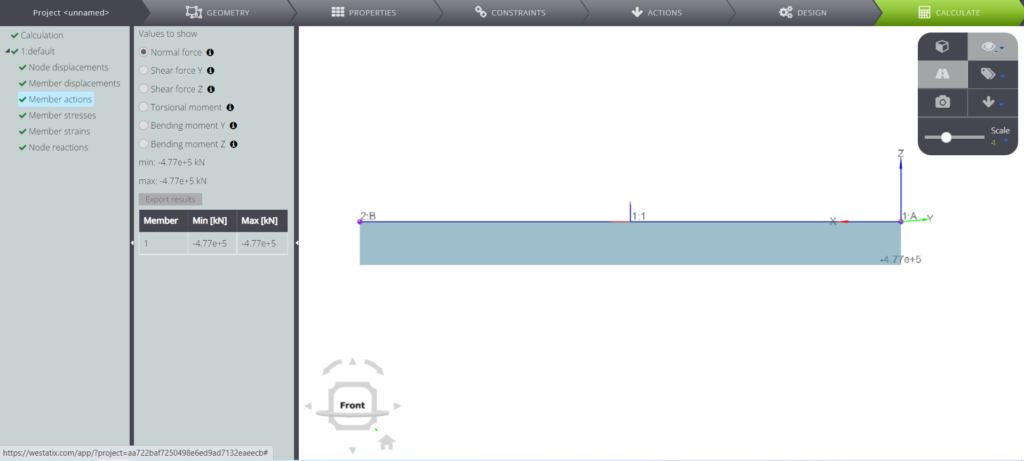
WeStatiX coglie perfettamente la soluzione.
[1] DARYL L. LOGAN, A First Course in the Finite Element Method, 4th edition, Thomson
