In questa sezione vogliamo verificare l’accuratezza di WeStatiX risolvendo il problema rappresentato nella figura sottostante. Esso consiste in una struttura a trave con spostamento imposto di un nodo supportato.
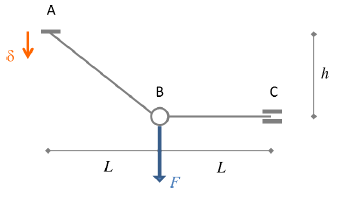
I dati necessari per realizzarlo sono riportati nella seguente tabella. È possibile inoltre consultare le istruzioni su come crearlo nei nostri tutorial.
| Modulo di Young | E | 200000000 | kPa |
| Sezione | A | 0,04 | \(m^2\) |
| Lunghezza | L | 4,00 | m |
| Altezza | h | 3,00 | m |
| Momento d’inerzia | J | 1,00E-04 | \(m^4\) |
| Spostamento | \(\delta\) | 0,001 | m |
Ecco il modello creato in WeStatiX, come mostrato in figura.
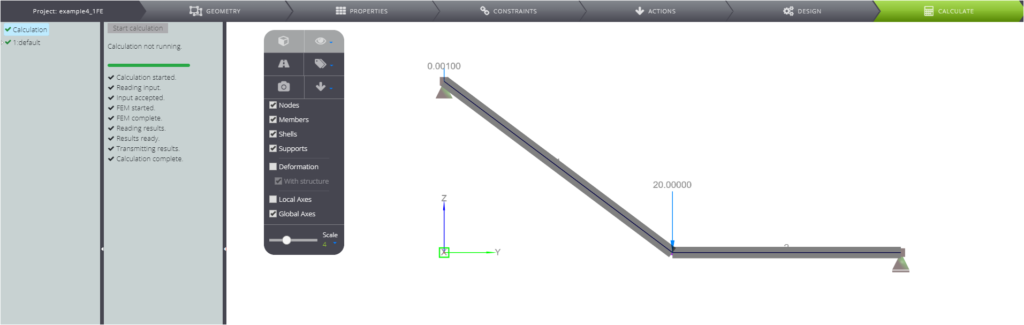
Come di consueto è possibile risolvere l’equazione della trave per trovare l’espressione di tutte le deformazioni, le rotazioni e le forze interne. Nella tabella seguente si confrontano i risultati fondamentali ottenuti analiticamente con i risultati numerici ottenuti in WeStatiX.
| DESCRIZIONE | PARAMETRO | UM | SOLUZIONE ANALITICA | WSX | Errore | |
|---|---|---|---|---|---|---|
| Reazione orizzontale in A | \(H_A\) | kN | \(\) | 0,00 | 0,00 | 0,00% |
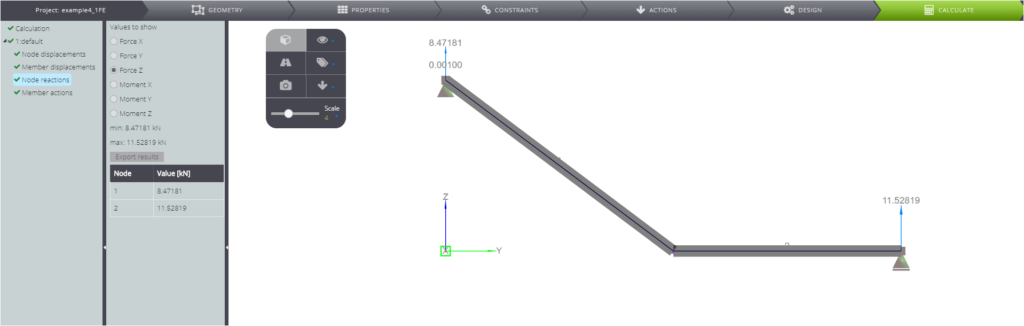
| Reazione verticale in A | \(V_A\) | kN | \(\) | 8,44 | 8,47 | 0,33% |
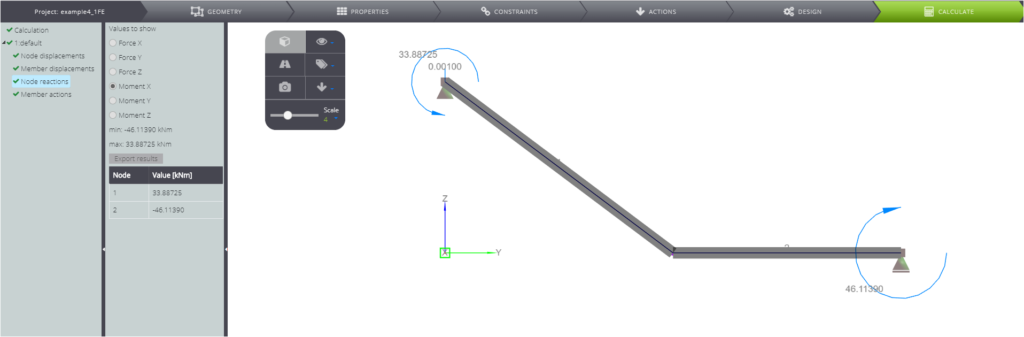
| Momento reagente in A | \(M_A\) | kNm | \(\) | 33,89 | 33,89 | 0,00% |
| Reazione verticale in C | \(V_C\) | kN | \(\) | 11,53 | 11,53 | 0,00% |
| Momento di reazione in C | \(M_C\) | kN | \(\) | -46,11 | -46,11 | 0,00% |
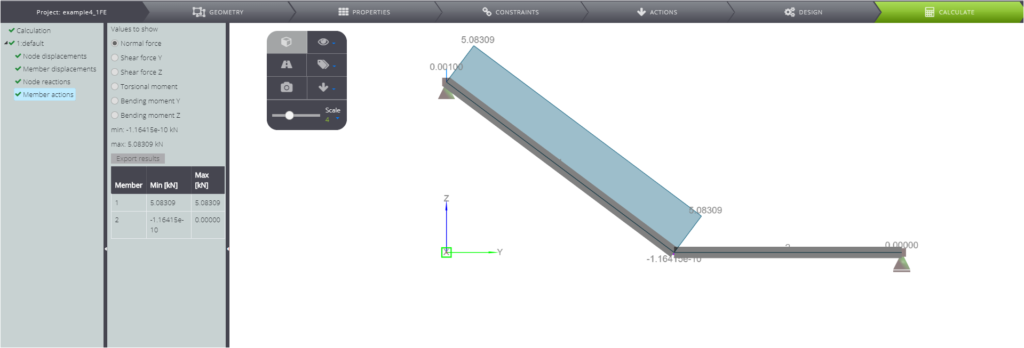
| Sforzo normale nella trave 1 | \(N_1\) | kNm | \(\) | 5,08 | 5,08 | 0,06% |
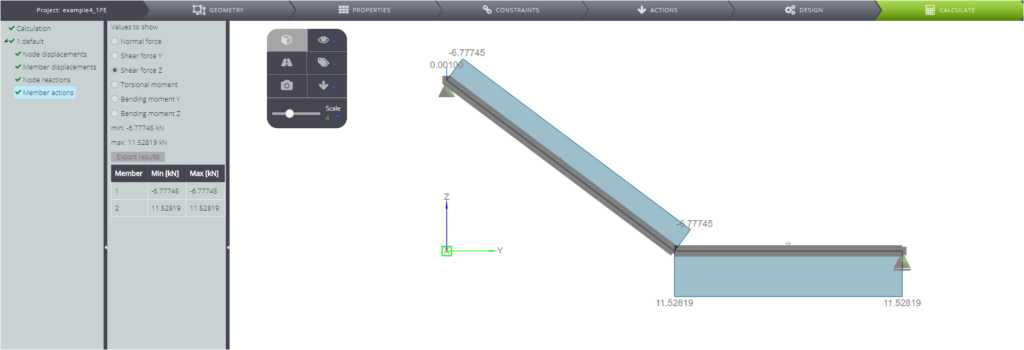
| Forza di taglio nella trave 1 | \(T_1\) | kN | \(\) | -6,78 | -6,78 | 0,04% |
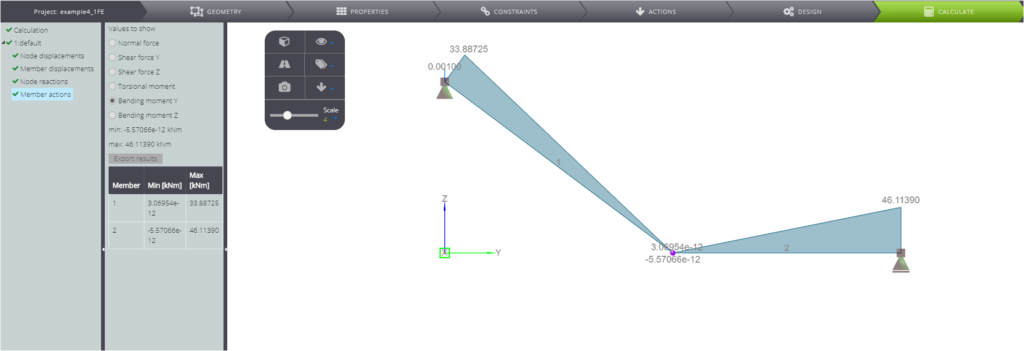
Nelle seguenti immagini si possono osservare tutti i risultati numerici.