Per testare il dimensionamento dei membri, consideriamo la trave rettangolare in cemento armato rappresentata qui sotto.
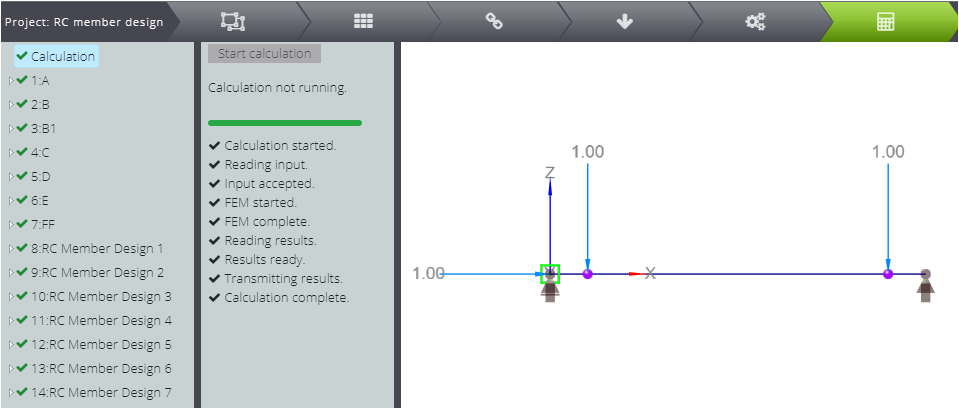
Si tratta di una trave di 10 m di lunghezza semplicemente appoggiata su due carichi puntiformi posizionati a 1 m di distanza dai supporti.
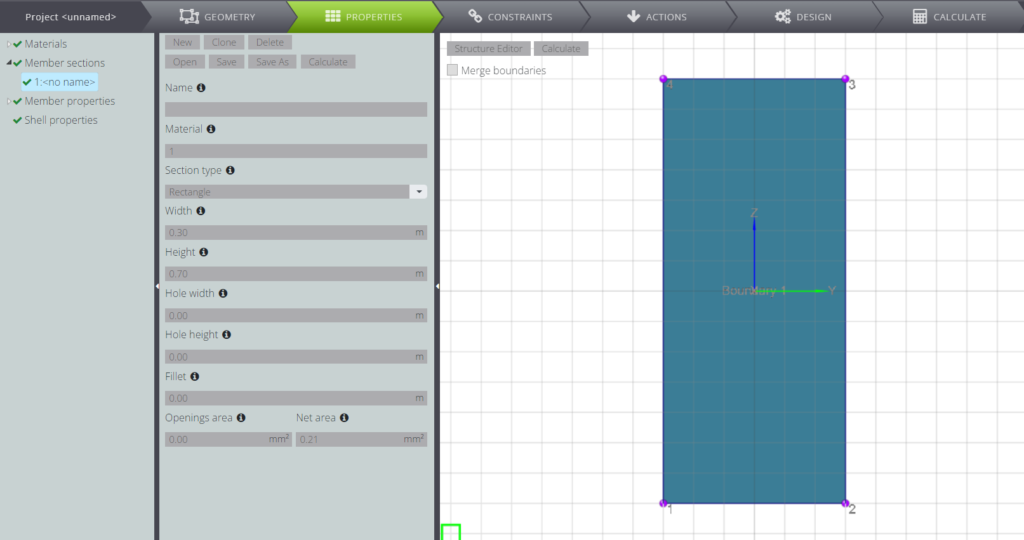
Le caratteristiche della sezione trasversale sono riportate nella seguente tabella.
| DESCRIZIONE | SIMBOLO | VALORE | UM | |
|---|---|---|---|---|
| Larghezza complessiva di una sezione trasversale | \(b\) | \(\) | 30,0 | cm |
| Altezza | \(h\) | \(\) | 70,0 | cm |
| Copriferro inferiore | \(c\) | \(\) | 50 | mm |
| Copriferro superiore | \(c’\) | \(\) | 50 | mm |
| Profondità effettiva della sezione trasversale | \(d\) | \(h-c\) | 65,0 | cm |
| \(z_S\) | \(h-c-c’\) | 60,0 | cm | |
| \(z_{s1}\) | \(h/2-c\) | 60,0 | cm | |
| \(z_{s2}\) | \(h/2-c’\) | 60,0 | cm |
Puoi anche trovare il modello in WeStatiX o imparare a costruirlo grazie al nostro tutorial.
RISULTATI
A questo punto, osserva attentamente i risultati: puoi esaminarli per ogni combinazione di carico e per ogni caso di progettazione di un membro in cemento armato. Essi saranno la combinazione lineare dei seguenti diagrammi.
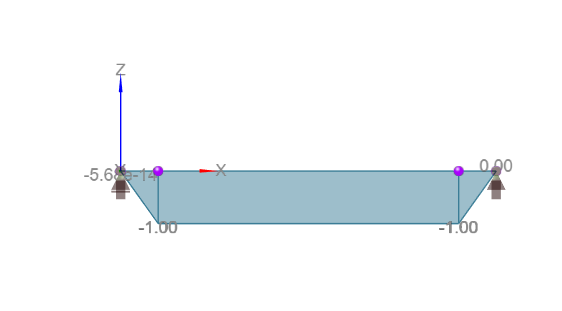
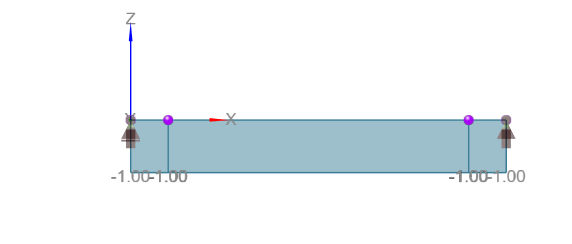
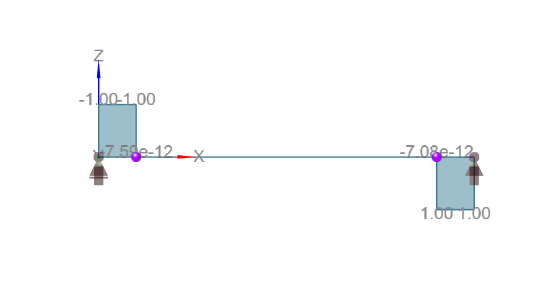
Come puoi vedere, il membro 2 non è mai soggetto alla forza di taglio. La progettazione della sezione della trave in cemento armato viene quindi eseguita solo per questo elemento per i sei casi indicati in tabella.
| CASE | A | B | C | D | E | F | ||
|---|---|---|---|---|---|---|---|---|
| Momento flettente [kNm] | \(M_{Ed}\) | 500 | 1500 | 1000 | 1000 | 400 | 300 | |
| Forza assiale [kN] | \(N_{Ed} \) | 0 | 0 | 1000 | 1800 | 2000 | 2000 |
In questo caso ci concentriamo sui risultati di progettazione dei membri RC e li confrontiamo con ciò che possiamo ottenere seguendo le linee guida della norma EN1992-1-1. [1]
I parametri del materiale sono elencati nella tabella sottostante.
| DESCRIZIONE | SIMBOLO | Formula | VALORE | UM |
|---|---|---|---|---|
| Resistenza caratteristica del cilindro di compressione del cemento a 28 giorni | \(f_{ck}\) | \(\) | 25.000 | kPa |
| Resistenza caratteristica di snervamento del rinforzo | \(f_{yk}\) | \(\) | 420.000 | kPa |
| Coefficiente per effetti a lungo termine | \(\alpha_{cc}\) | \(\) | 1,00 | – |
| Coefficiente di sicurezza per calcestruzzo | \(\gamma_c\) | \(\) | 1,50 | – |
| Coefficiente di sicurezza per l’acciaio di armatura o precompresso | \(\gamma_s\) | \(\) | 1,15 | – |
| Valore di progetto della resistenza a compressione del cemento | \(f_{cd}\) | \(\alpha_{cc} f_{ck}/\gamma_c\) | 16.670 | kPa |
| Valore di progetto per la resistenza allo snervamento dell’armatura | \(f_{yd}\) | \(f_{yk}/\gamma_{s}\) | 365.220 | kPa |
Nei grafici si possono osservare i rapporti sforzo-deformazione per il cemento e per l’acciaio d’armatura.
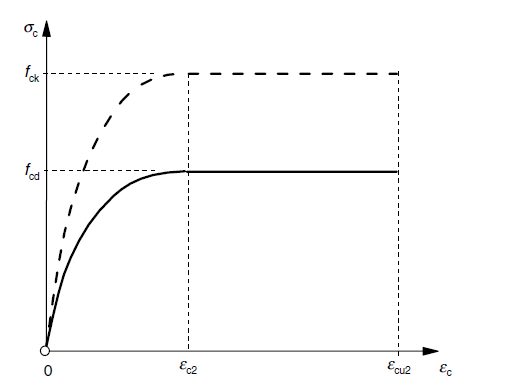
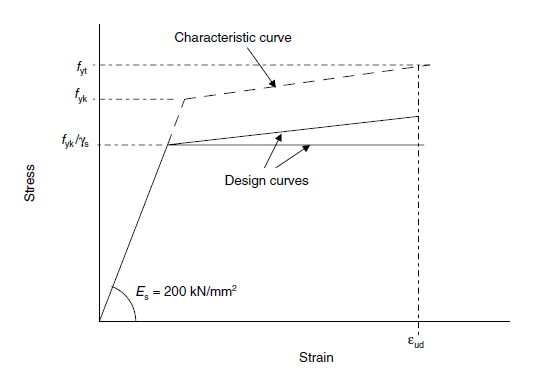
Dati i parametri del materiale e le caratteristiche della sezione si possono calcolare i seguenti parametri.
| \(x_{lim}\) | \(\frac{700 \cdot d}{f_{yd [MPa]}+700}\) | 42,71 | cm | |
| \(F_{cd,lim}\) | \(0,8095 \cdot x_{lim} \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Essi consentono di definire le varie condizioni di stress sulle sezioni trasversali.
CASO A
Nel primo caso, la parte centrale della trave è sottoposta a condizioni di flessione pura.
| Momento flettente | \(M_{Ed}\) | \(\) | 500 | kNm |
| Forza assiale | \(N_{Ed}\) | \(\) | 0 | kN |
Per calcolare l’area di rinforzo è necessario calcolare il seguente parametro, come descritto in [1].
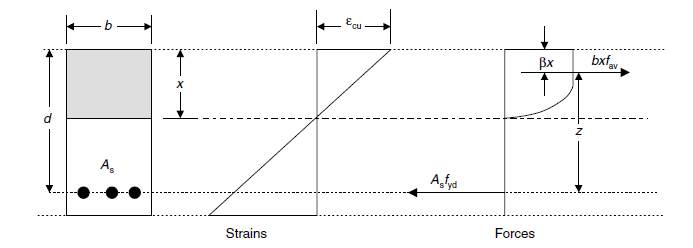
| DESCRIZIONE | SIMBOLO | Formula | VALORE | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{s1} =M_{Ed}\) | 500 | kNm | |
| Profondità dell’asse neutro | \(x\) | \(1,202\left(d-\sqrt{d^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | 22,1 | cm |
| \(x<x_{lim}\) | ||||
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 895,99 | kN | |
| \(M_{cd1}\) | \(F_{cd}\cdot(d-0,4160x)\) | 499,88 | kNm |
In questo caso la trave è rinforzata da un solo lato e si può calcolare facilmente la soluzione per la sezione trasversale dell’acciaio di armatura.
| ANALITICO | WSX | ERRORE | |||
|---|---|---|---|---|---|
| Sezione trasversale dell’armatura (inferiore) [cm^2] | \(A_{s1}’\) | \(\frac{F_{cd}-N}{f_{yd}}\) | 24,53 | 24,54 | 0,04% |
I risultati per la progettazione del membro in cemento armato sono mostrati nella figura seguente.
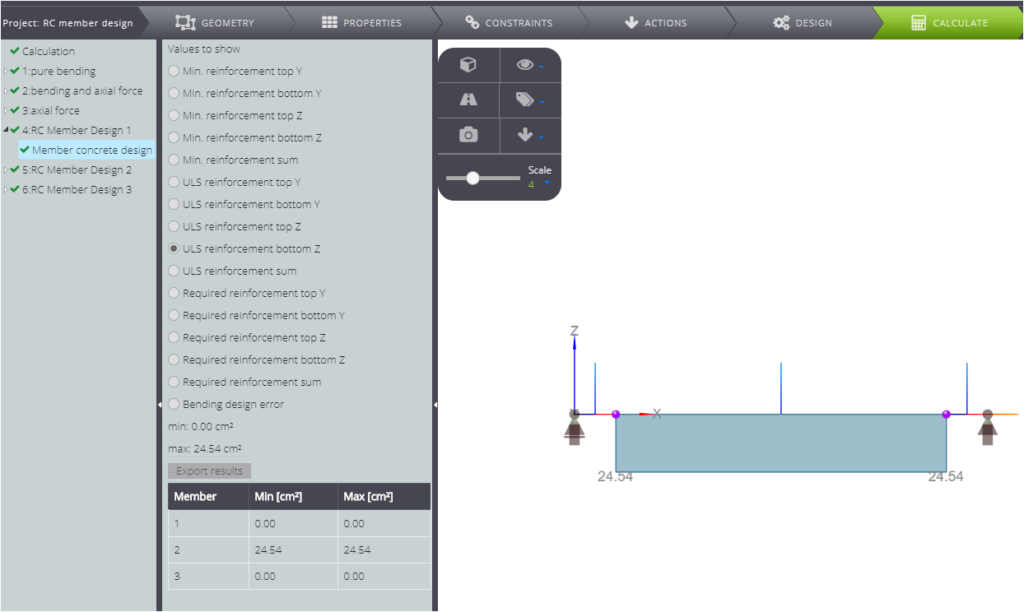
Corrisponde perfettamente ai risultati che abbiamo ottenuto seguendo lo standard.
CASO B
Come nel caso A la forza assiale è nulla, ma il momento flettente è maggiore.
| Momento flettente | \(M_{Ed}\) | \(\) | 1500 | kNm |
| Forza assiale | \(N_{Ed}\) | \(\) | 0 | kN |
Questo conduce al seguente calcolo.
| DESCRIZIONE | SIMBOLO | Formula | VALORE | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{s1} =M_{Ed}\) | 1500 | kNm | |
| Profondità dell’asse neutro | \(x\) | \(1,202\left(d-\sqrt{d^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | – | cm |
| \(\sqrt{\cdot}<0\) | ||||
| Profondità dell’asse neutro | \(x\) | \(x=x_{lim}\) | 42,71 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Data la maggiore entità del momento flettente, in questo caso sarà necessaria un’ area di rinforzo anche sulla parte superiore della sezione trasversale. È possibile calcolare l’area della sezione trasversale per l’armatura inferiore e superiore e confrontarla con i risultati di WeStatiX.
| ANALITICO | WSX | ERRORE | |||
|---|---|---|---|---|---|
| Sezione trasversale dell’armatura (inferiore) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 78,53 | 78,53 | 0,00% |
| Sezione trasversale dell’armatura (superiore) [cm^2] | \(A_{s2}\) | \(\frac{M_{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 31,19 | 31,19 | 0,00% |
Come potete vedere, le due soluzioni combaciano.
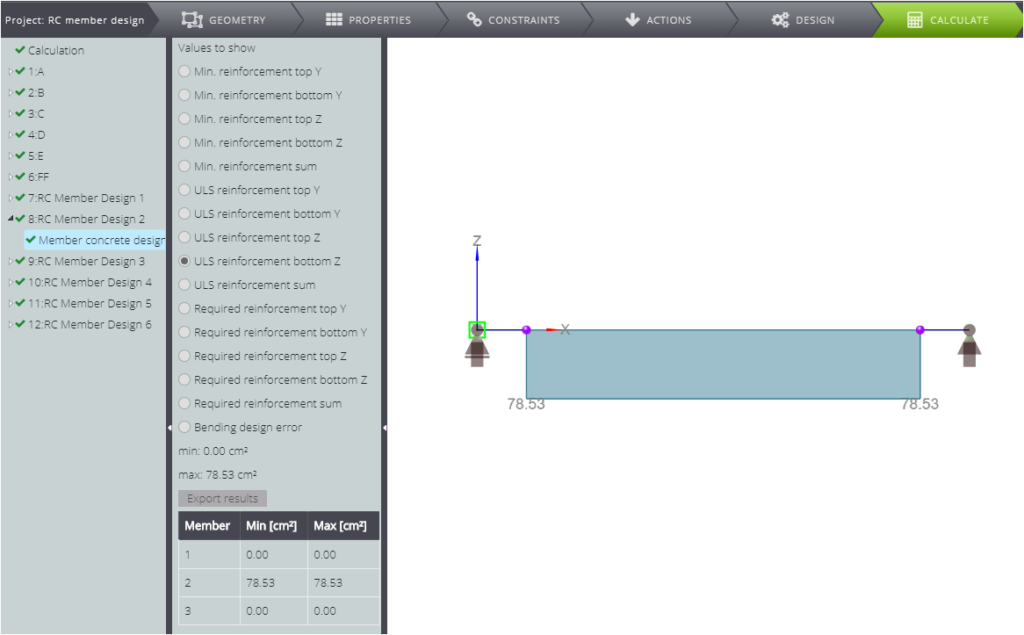
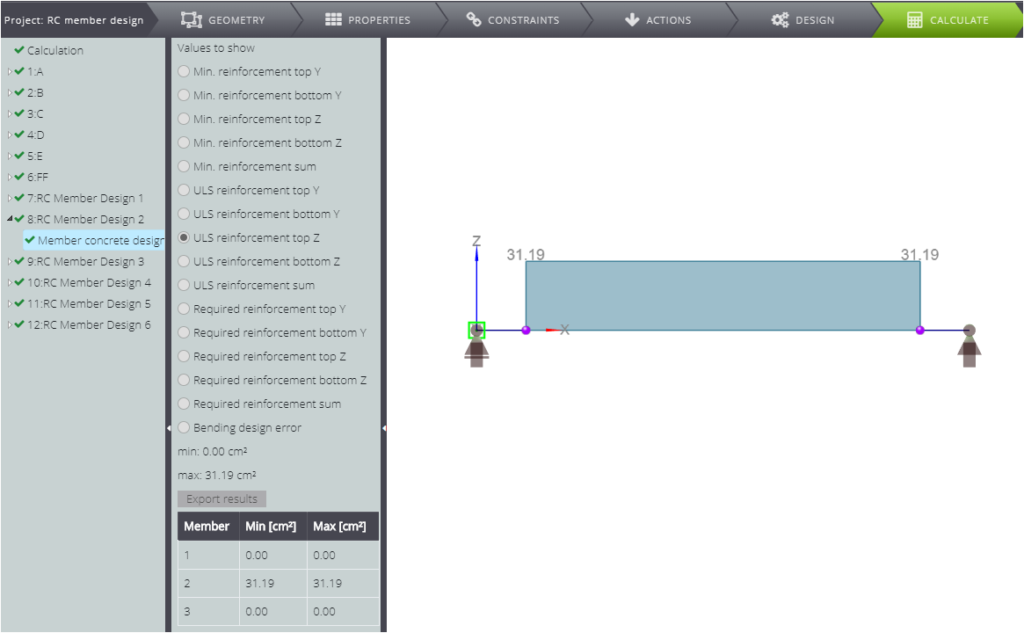
CASO C
In questo caso lo sforzo della sezione trasversale dipende dal momento flettente, ma anche dalla forza assiale.
| Momento flettente | \(M_{Ed}\) | \(\) | 1000 | kNm |
| Forza assiale | \(N_{Ed}\) | \(\) | 1000 | kN |
Per calcolare l’area di rinforzo, è necessario calcolare i parametri visualizzati nella tabella.
| DESCRIZIONE | SIMBOLO | Formula | VALORE | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{s1} =M_{Ed}+N_{Ed}\cdot z_{s1}\) | 1300 | kNm | |
| Profondità dell’asse neutro | \(x\) | \(1,202\left(d-\sqrt{d^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | – | cm |
| \(\sqrt{\cdot}<0\) | ||||
| Profondità dell’asse neutro | \(x\) | \(x=x_{lim}\) | 42,71 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Ora, come nel caso precedente, è possibile calcolare le aree di rinforzo e confrontarle con i risultati numerici.
| ANALITICO | WSX | ERRORE | |||
|---|---|---|---|---|---|
| Sezione trasversale dell’armatura (inferiore) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 42,02 | 42,01 | 0,02% |
| Sezione trasversale dell’armatura (superiore) [cm^2] | \(A_{s2}\) | \(\frac{M_{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 22,06 | 22,05 | 0,05% |
Anche in questo caso si verifica la soluzione WeStatiX per la progettazione di una trave in cemento armato.
CASO D
Ora guardiamo lo stato di carico quando si aumenta la forza assiale.
| Momento flettente | \(M_{Ed}\) | \(\) | 1000 | kNm |
| Forza assiale | \(N_{Ed}\) | \(\) | 1800 | kN |
A differenza del caso precedente la forza di compressione \(N > F_{cd,lim} \)
Anche in questo caso, calcolare i seguenti parametri.
| DESCRIZIONE | SIMBOLO | Formula | VALORE | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{Ed}+N_{Ed}\cdot z_{s1}\) | 1540 | kNm | |
| \(M_{S2}\) | \(M_{s2} =M_{Ed}-N_{Ed}\cdot z_{s2}\) | 460 | kNm | |
| Profondità dell’asse neutro | \(x\) | \(1,202\left(c’-\sqrt{c’^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | – | cm |
| \(\sqrt{\cdot}<0\) | ||||
| Profondità dell’asse neutro | \(x\) | \(x=x_{lim}\) | 42,71 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
E infine, calcolare le sezioni trasversali per il rinforzo.
| ANALITICO | WSX | ERRORE | |||
|---|---|---|---|---|---|
| Sezione trasversale dell’armatura (inferiore) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 31,06 | 31,07 | 0,03% |
| Sezione trasversale dell’armatura (superiore) [cm^2] | \(A_{s2}\) | \(\frac{M{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 33,01 | 33,01 | 0,00% |
Se lo si confronta con il risultato di WeStatiX del modello per la progettazione di travi in cemento armato, si può notare che i valori sono gli stessi.
CASO E
Ora si riduce il momento flettente.
| Momento flettente | \(M_{Ed}\) | \(\) | 400 | kNm |
| Forza assiale | \(N_{Ed}\) | \(\) | 2000 | kN |
Per definire lo stato di carico, definire i parametri elencati nella tabella.
| DESCRIZIONE | SIMBOLO | Formula | VALORE | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{Ed}+N_{Ed}\cdot z_{s1}\) | 1000 | kNm | |
| \(M_{S2}\) | \(M_{s2} =M_{Ed}-N_{Ed}\cdot z_{s2}\) | -200 | kNm | |
| Profondità dell’asse neutro | \(x\) | \(1,202\left(c’-\sqrt{c’^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | 41,0 | cm |
| \(x<x_{lim}\) | ||||
| Profondità dell’asse neutro | \(x\) | \(x=x_{lim}\) | 42,7 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
È ancora necessaria un’area di rinforzo sia nella parte superiore che in quella inferiore della sezione. Si calcola nel modo seguente.
| ANALITICO | WSX | ERRORE | |||
|---|---|---|---|---|---|
| Sezione trasversale dell’armatura (inferiore) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 0,95 | 0,95 | 0,00% |
| Sezione trasversale dell’armatura (superiore) [cm^2] | \(A_{s2}\) | \(\frac{M{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 8,37 | 8,37 | 0,00% |
Anche in questo caso le due soluzioni coincidono perfettamente.
CASO F
Come si può leggere nella seguente tabella, rispetto al CASO D con la stessa forza assiale, il momento flettente è minore.
| Momento flettente | \(M_{Ed}\) | \(\) | 300 | kNm |
| Forza assiale | \(N_{Ed}\) | \(\) | 2000 | kN |
Quando si calcola il seguente parametro, si può notare che, come applicato ai casi precedenti, la profondità dell’asse neutro è maggiore di \(x_{lim}\)
| DESCRIZIONE | SIMBOLO | Formula | VALORE | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{Ed}+N_{Ed}\cdot z_{s1}\) | 900 | kNm | |
| \(M_{S2}\) | \(M_{s2} =M_{Ed}-N_{Ed}\cdot z_{s2}\) | -300 | kNm | |
| Profondità dell’asse neutro | \(x\) | \(1,202\left(c’-\sqrt{c’^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | 48,6 | cm |
| \(x>x_{lim}; x<h\) | ||||
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.968,82 | kN |
Ciò implica che è necessaria solo l’area di armatura superiore.
| ANALITICO | WSX | ERRORE | |||
|---|---|---|---|---|---|
| Sezione trasversale dell’armatura (superiore) [cm^2] | \(A_{s2}’\) | \(\frac{N-F_{cd}}{f_{yd}}\) | 0,85 | 0,85 | 0,00% |
Anche in questo caso, i risultati di WeStatiX corrispondono a quelli analitici.
[1] Skriptum zur Vorlesung BETONBAU 1 nach EC 1992-1-1, Technische Universität Wien, Institut für Tragkonstruktionen – Herausgegeben von Prof. Dr.-Ing. Johann KOLLEGER
