In questo caso si considera una piastra circolare di raggio a: essa sostiene un carico di intensità q uniformemente distribuito su tutta la sua superficie, mentre i bordi sono bloccati.
| Modulo di Young | E | 1,00E08 | kPa |
| Spessore | h | 1,00 | m |
| Modulo di Poisson | \(\nu\) | 0,30 | – |
| Raggio | a | 10,00 | m |
| Pressione uniforme | q | -10,00 | kPa |
| Rigidità flessionale della piastra | D | 9157509,16 | kN/m |
La rigidità flessionale della piastra è pari a \(D = {E \cdot h^3}/{12(1-\nu^2)}\).
È possibile consultare come abbiamo costruito il modello in WeStatiX nella nostra documentazione. Troverai anche le dimensioni e le costanti dei materiali. In alternativa, è possibile trovarlo tra i nostri tutorial.
La soluzione analitica di questo problema è data nella “Theory of plates and shells”, [1].
Se \(D= \frac{E h^3}{12 (1-\nu^2)}\) è la rigidità della piastra, si prevede che la deviazione sia \(w(x)= \frac{q}{64D} (a^2-r^2)^2\)
I momenti flettenti sono invece:
\(M_r= \frac{q}{16} [a^2(1+\nu)-r^2 (3+\nu); \) è il momento flettente che agisce lungo le sezioni circonferenziali della piastra.
\(M_t= \frac{q}{16} [a^2(1+\nu)-r^2 (1+3\nu)\) è il momento flettente che agisce lungo le sezioni diametrali della piastra.
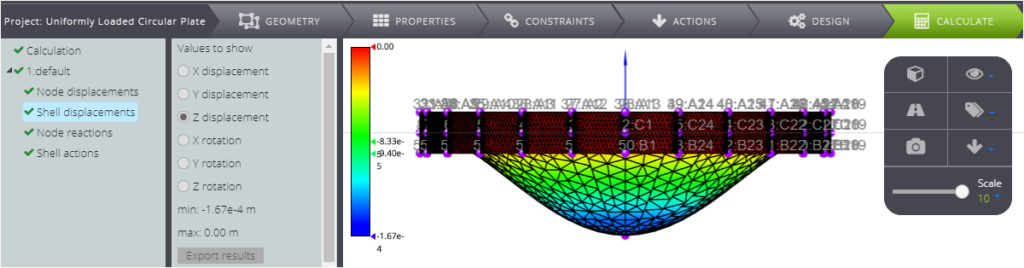
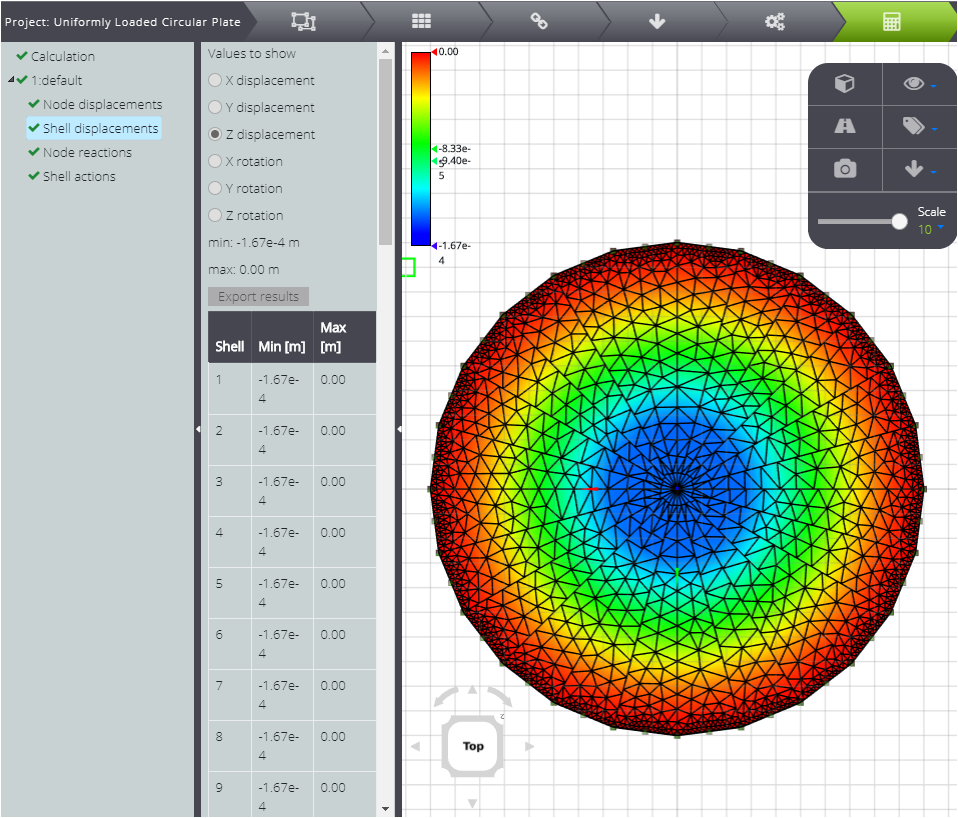
Avvia l’analisi nella scheda CALCULATE, in modo da poter visualizzare i risultati dei contorni come nelle immagini sottostanti.
Si ricorda che si riferiscono agli assi globali.
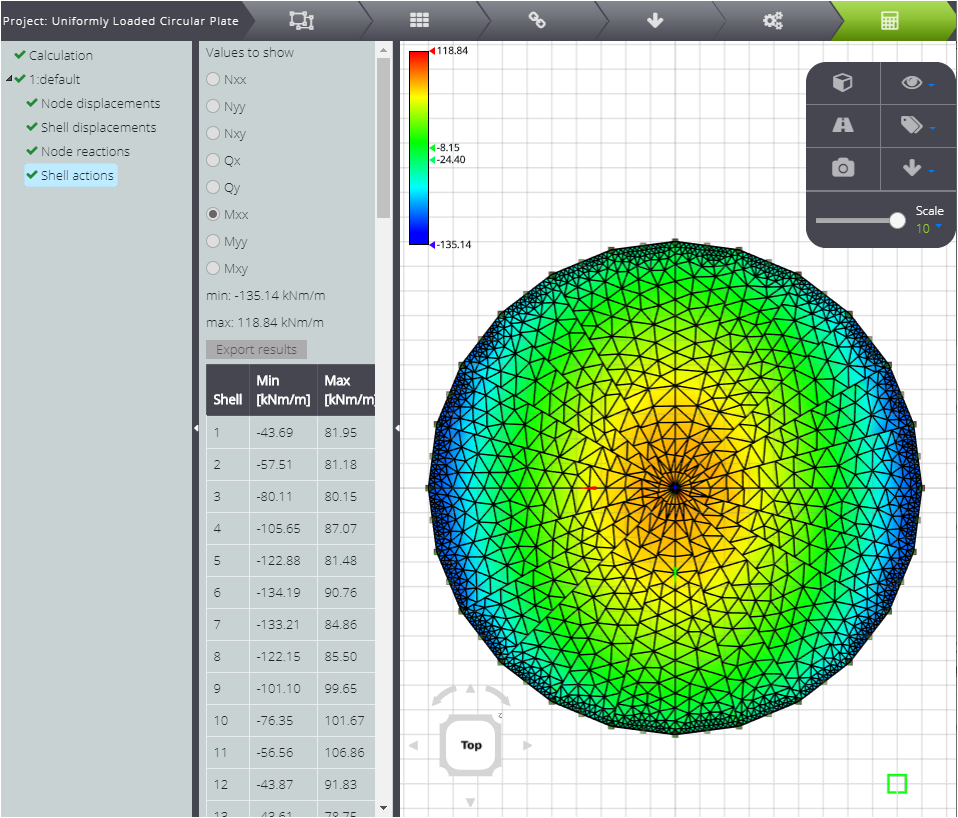
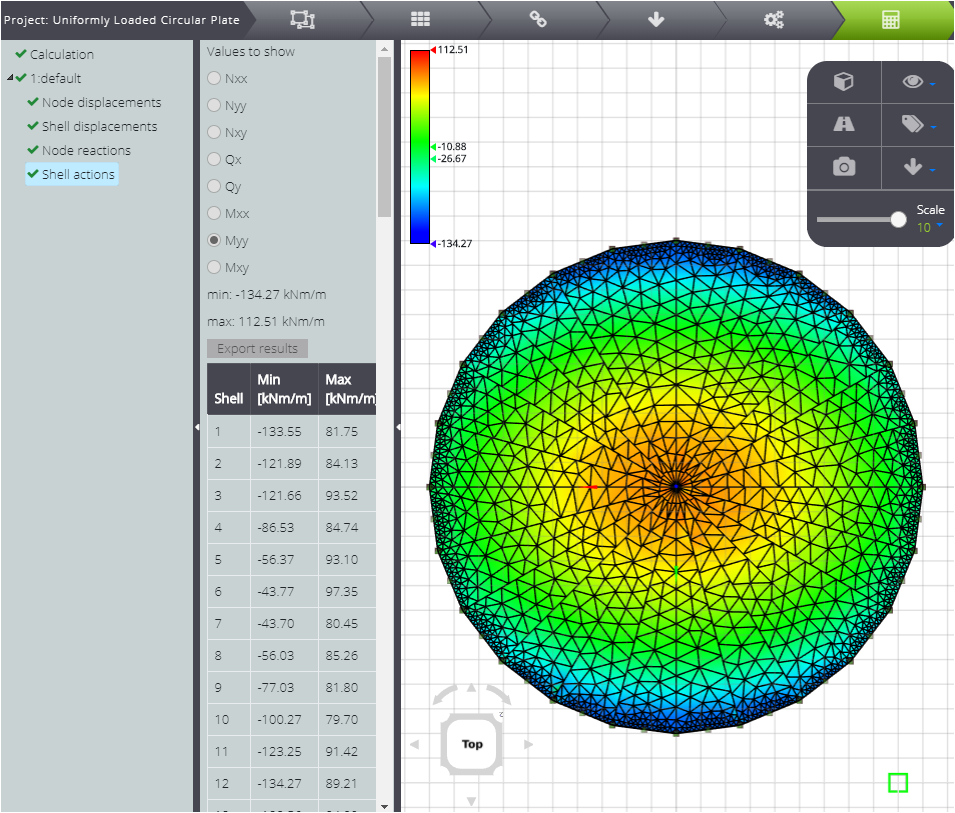
Per poter confrontare la soluzione numerica con quella analitica, è possibile esportare i risultati e tracciarne il grafico. In questo modo potrà essere visualizzato il confronto tra le due soluzioni .
In primo luogo, gli spostamenti.
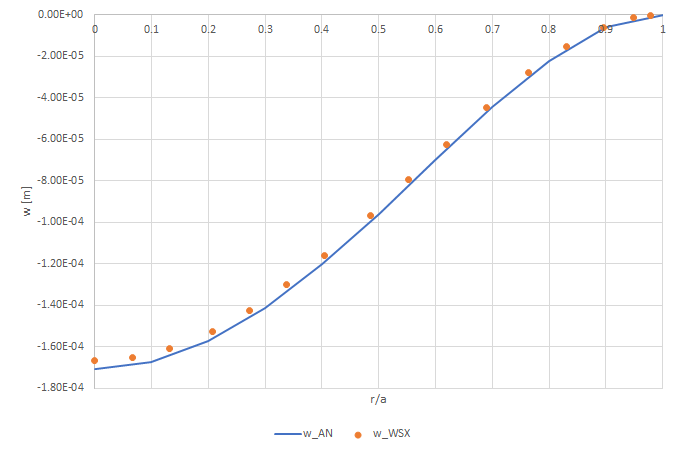
In secondo luogo, il momento flettente \(M_r\).
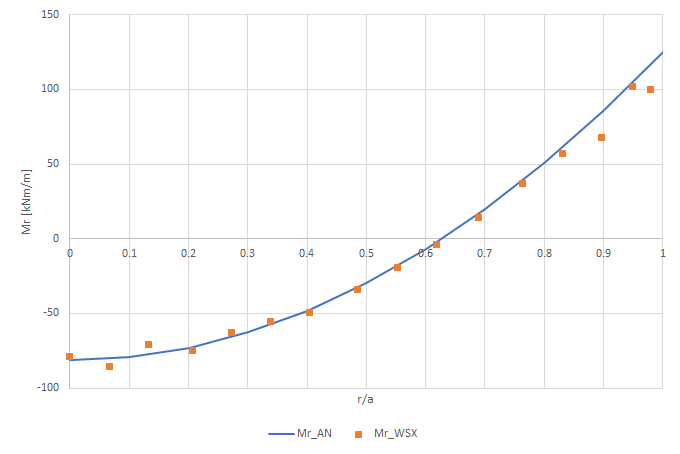
Per ultimo, il momento flettente \(M_t\)
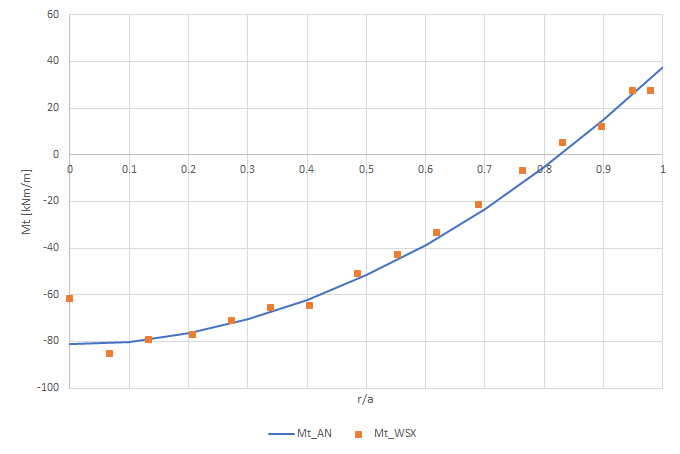
[1] TIMOSHENKO S., WOINOWSKY Y-RIEGER S., Theory of plates and shells, 2ed., McGraw-Hill, New York, 1959
