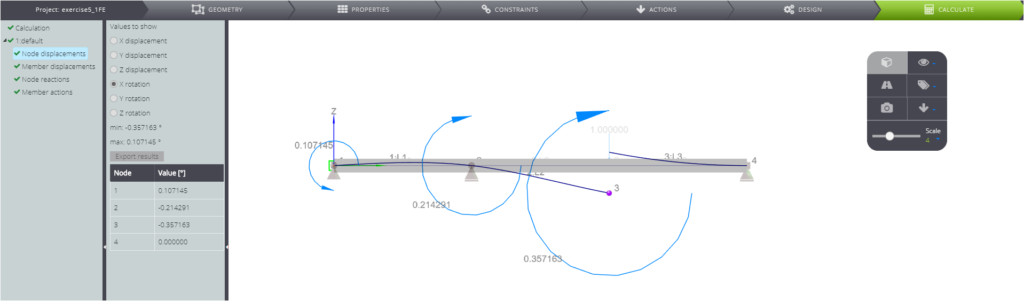
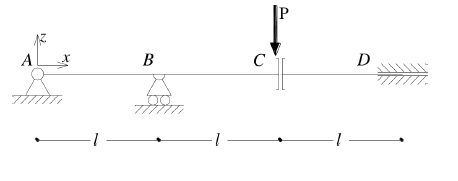
In questa pagina si confrontano i risultati analitici con quelli ottenuti con WeStatiX per il sistema rappresentato di seguito: si tratta di una trave continua con rotazione vincolata e rilascio dello spostamento verticale sotto un carico puntiforme.
Nella tabella è possibile consultare i dati necessari per costruire il modello. Spieghiamo anche come realizzarlo nei nostri tutorial.
| Modulo di Young | E | 1,00 | kPa |
| Sezione | A | 0,01 | \(m^2\) |
| Lunghezza | L | 1,00 | m |
| Momento d’inerzia | J | 1,00 | \(m^4\) |
| Carico | P | -1,00 | \(kN\) |
Ecco il modello FE: si trova nella libreria di WeStatiX
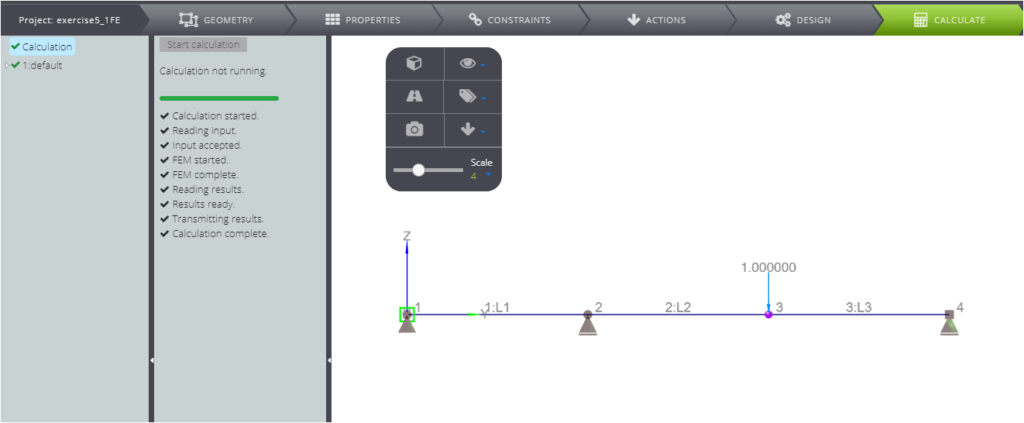
Come per gli esempi precedenti, vogliamo dimostrare la precisione di WeStatiX confrontando la soluzione analitica (che si può ottenere con l’equazione della trave) con quella numerica. Trovi tutto nella tabella seguente.
| DESCRIZIONE | PARAMETRO | UM | SOLUZIONE ANALITICA | SOLUZIONE ANALITICA | WSX | Error |
|---|---|---|---|---|---|---|
| Rotazione in A | \(\phi_{A}\) | rad | \(3PL^2/28EJ\) | 0,10714 | 0,10715 | 0,00% |
| Rotazione in B | \(\phi_B\) | rad | \(3PL^2/14EJ\) | -0,21429 | -0,21429 | 0,00% |
| Rotazione in C | \(\phi_C\) | rad | \(5PL^2/14EJ\) | -0,35714 | -0,35716 | 0,01% |
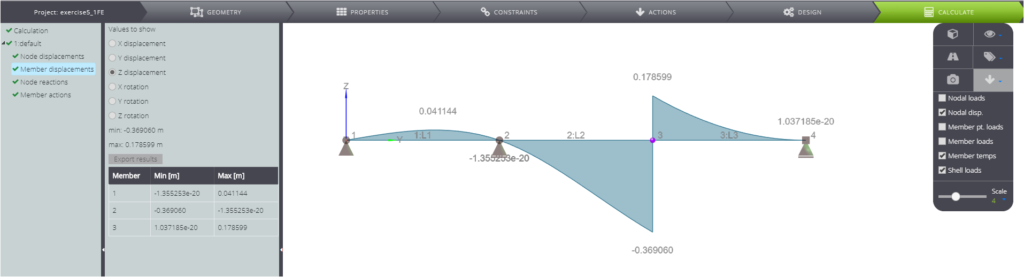
| Spostamento verticale in C (sinistra) | \(v_c^{l}\) | m | \(31PL^3/84EJ\) | -0,36905 | -0,36906 | 0,00% |
| Spostamento verticale in C (destra) | \(v_c^{r}\) | m | \(5PL^3/28EJ\) | 0,17857 | 0,17860 | 0,02% |
| Momento flettente in C | \(M_C\) | kNm | \(5PL/14\) | 0,35714 | 0,35713 | 0,00% |
| Forza di taglio in A | \(T_A\) | kN | \(9P/14\) | 0,64286 | 0,64287 | 0,00% |
| Forza di taglio in C | \(T_C\) | kN | \(1P/1\) | -1,00000 | -1,00000 | 0,00% |
Di seguito alcuni screeshot dei risultati.