Müssen Sie ein Stahlbetonelement unter biaxialer Biegung bemessen? In diesem Beispiel sehen Sie, wie wir die Genauigkeit von WeStatiX bei der Berechnung der Bewehrungsquerschnittsfläche für einen Träger unter zweiachsiger Biegung validieren.
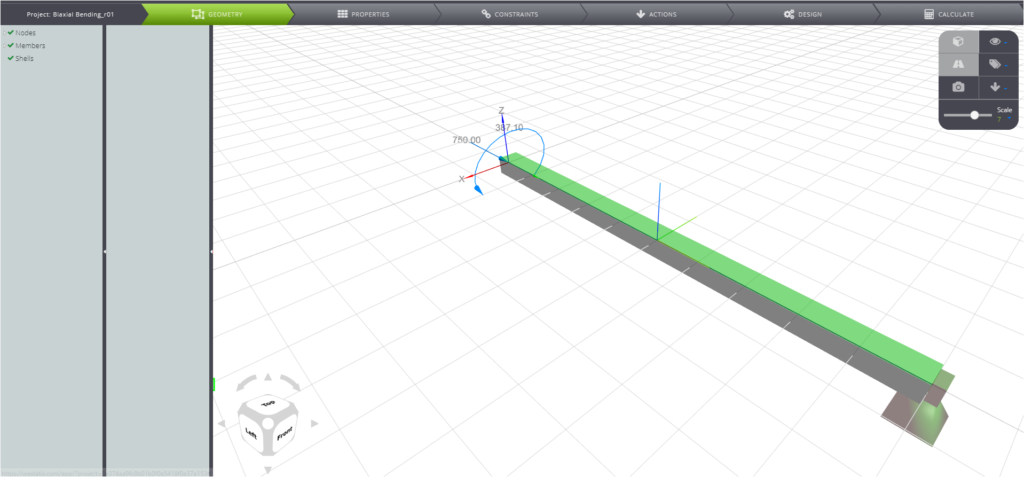
In WeStatiX finden Sie das Modell, das wir für diese Verifizierung verwendet haben: Es handelt sich um einen Kragbalken, der an seinem freien Ende einer biaxialen Biegung und einer axialen Druckkraft ausgesetzt ist.
| Normalkraft | \(N_{Ed}\) | \(\) | 750 | kN |
| Biegemoment X | \(M_{Ed,X}\) | \(\) | 225 | kNm |
| Biegemoment Z | \(M_{Ed,Z}\) | \(\) | 315 | kNm |
Die Querschnittseigenschaften sind nachstehend aufgeführt.
| BESCHREIBUNG | Symbol | WERT | UM | |
|---|---|---|---|---|
| Gesamtbreite des Querschnitts | \(b\) | \(\) | 500 | mm |
| Höhe | \(h\) | \(\) | 400 | mm |
| Betondeckung | \(d_1\) | \(\) | 70 | mm |
| Betondeckung | \(d_2\) | \(\) | 70 | mm |
| \(d’\) | \(h-d_1\) | 330 | mm | |
| – | \(b’\) | \(b-d_2\) | 430 | mm |
| Verhältnis für die Wahl des Interaktionsdiagramms | \(d’/h\) | \(\) | 0,18 | – |
Und schließlich die Materialparameter
| BESCHREIBUNG | Symbol | WERT | UM | |
|---|---|---|---|---|
| Charakteristische Zylinderdruckfestigkeit von Beton nach 28 Tagen | \(f_{ck}\) | \(\) | 25.000,00 | kPa |
| Charakteristische Fließgrenze der Bewehrung | \(f_{yk}\) | \(\) | 550.000,00 | kPa |
| Koeffizient unter Berücksichtigung von Langzeiteffekten | \(\alpha_{cc}\) | \(\) | 1,00 | – |
| Teilfaktor für Beton | \(\gamma_c\) | \(\) | 1,50 | – |
| Teilfaktor für Betonstahl | \(\gamma_s\) | \(\) | 1,15 | – |
| Bemessungswert der Betondruckfestigkeit | \(f_{cd}\) | \(\alpha_{cc} f_{ck}/\gamma_c\) | 16.666,67 | kPa |
| Bemessungswert für die Fließgrenze der Bewehrung | \(f_{yd}\) | \(f_{yk}/\gamma_{s}\) | 478.260,87 | kPa |
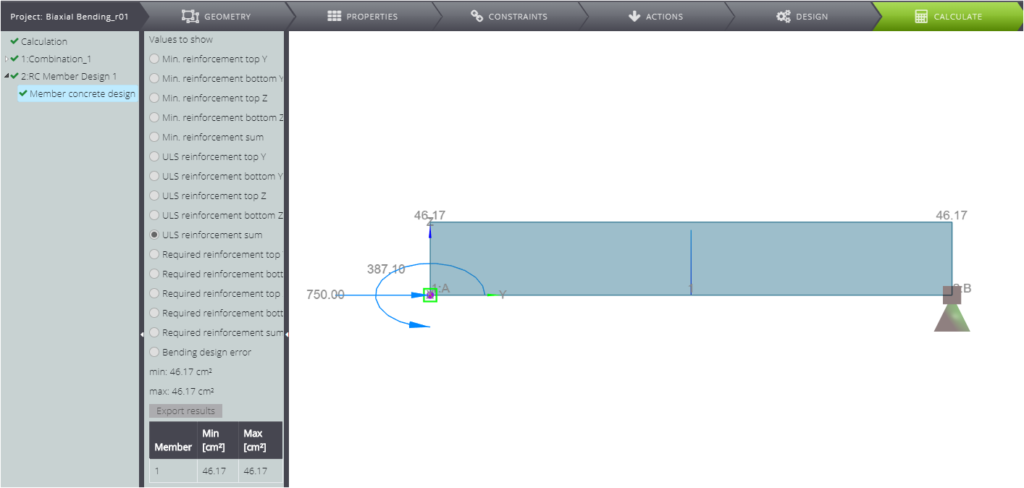
Wenn das Modell fertig ist, können Sie mit der Analyse beginnen, und Sie erhalten die folgenden Diagramme.
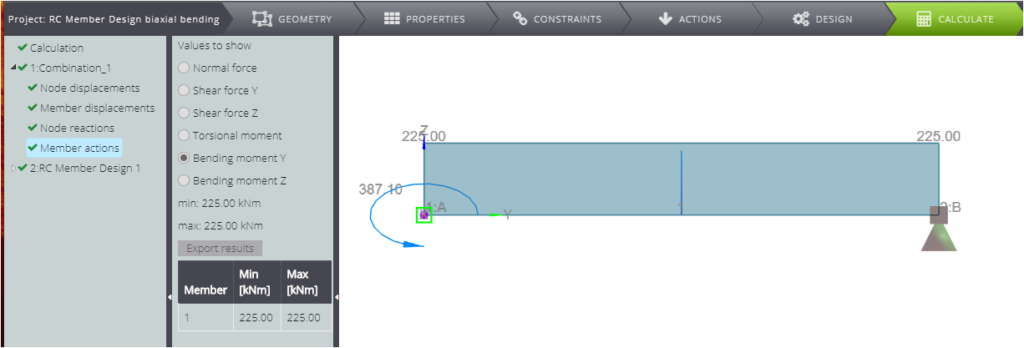
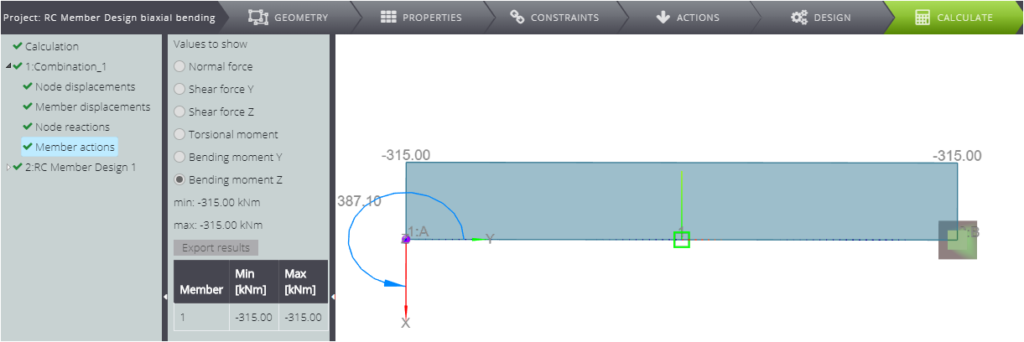
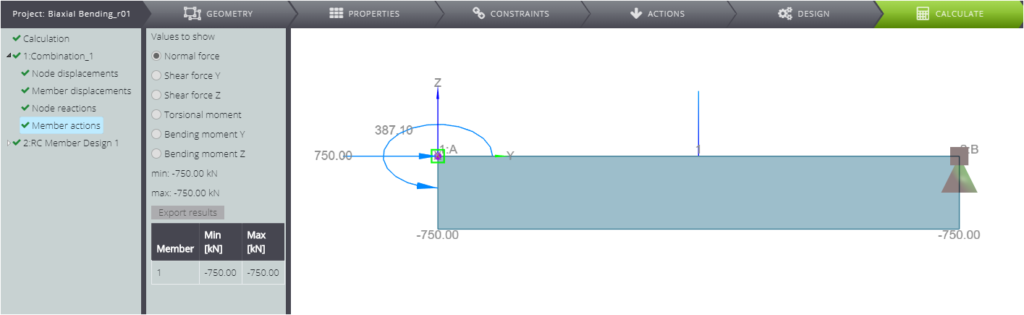
Wenn Sie sich auf die Ergebnisse der Bemessung von Stahlbetongliedern konzentrieren, können Sie sehen, dass die Gesamtbewehrungsfläche im Querschnitt \(A_{s,tot}=46,17cm^2\) beträgt.
Mit den Interaktionsdiagrammen für die Stahlbetonbemessung eines Querschnitts unter zweiachsiger Biegung können Sie dies kurz verifizieren. [1]
| Parametrisierte Axialkraft | \(\nu\) | \(N_d/b \cdot h \cdot f_{cd}\) | 0,225 | – |
| \(\beta\) | \(0,6+\nu\) | 0,825 | – | |
| Fiktive Exzentrizität | \(e’_y\) | \(e_y + \beta \cdot e_z \cdot b / h\) | 0,733 | m |
| Wirksames uniaxiales Moment | \(M’_z\) | \(N_{Ed}\cdot e’_y\) | 549,84 | kNm |
| Parametriertes Biegemoment | \(\mu\) | \(M’_z/b\cdot h^2 \cdot f_{cd}\) | 0,33 | – |
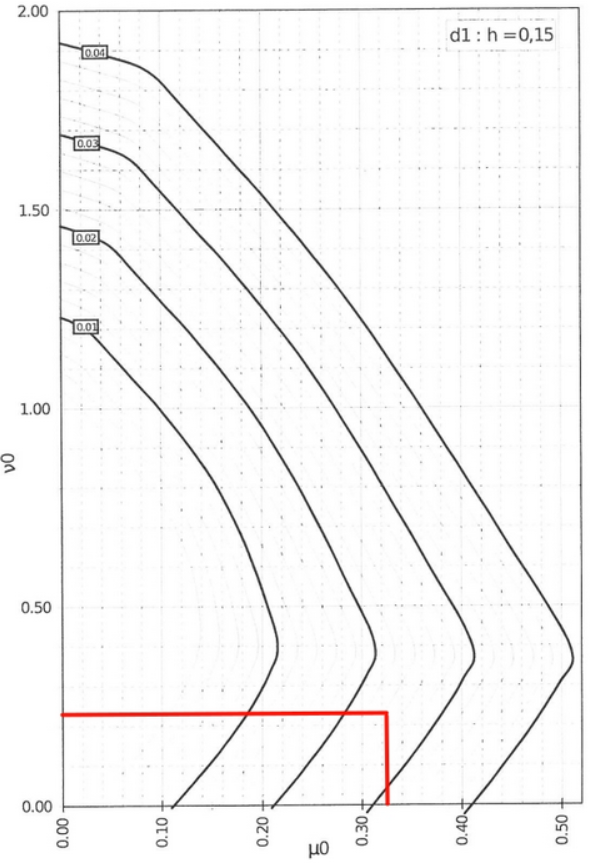
| Koeffizient aus Interaktionsdiagramm | \(A_s / b \cdot h\) | \(\) | 0,02 | – |
| Gesamtbewehrungsfläche | \(A_{s,tot}\) | \(\) | 48,00 | cm^2 |
Der Fehler ist also
\( \epsilon = 1-\frac{46,17}{48,00} = 3,81\% \)Was akzeptabel ist, da die Interaktionsdiagramm-Methode approximativ ist. Die Lösung von WeStatiX ist daher verifiziert.
[1] Scriptum zur Vorlesung BETONBAU 1 nach EC 1992-1-1, Technische Universität Wien, Institut für Tragkonstruktionen – Herausgegeben von Prof. Dr.-Ing. Johann KOLLEGER
