Mit diesem Tutorial zeigen wir Ihnen, wie man eine kreisförmige Platte mit Radius a und Dicke h modelliert, die an den Rändern unter gleichmäßiger Belastung q eingespannt ist. Wenn Sie dieses Modell laden und alle Details sehen möchten, finden Sie es in den öffentlichen Projekten von WestatiX.
Der Start der Simulation dieses Tutorials erfordert einige Funktionen, die im WeStatiX Free Plan möglicherweise nicht verfügbar sind. Sie können den Plan jederzeit ändern.
Die Problemdaten sind unten aufgeführt:
Radius \( a = 10 m \) ;
Dicke \( h = 1 m \) ;
Young-Modul \( E = 10^8 kPa \) ;
Poisson Koeffizient \( \nu= 0.3 \) ;
Druck \( q = -10 kPa \).
Geometrie
Beginnen Sie mit der Erstellung der Knoten! Drücken Sie dann auf die Registerkarte GEOMETRIE und wählen Sie Knoten im Entity Tree.
Wir erstellen einen in der Mitte der Platte und dann weitere am Rand der Platte, wobei wir der Vorgangweise folgen:
\( x_i = a sen \theta_i ;\\ y_i = a cos \theta_i \)Und \( \theta_i = \theta_{i-1} + \Delta \theta \).
Für dieses Beispiel haben wir ein Intervall \( \Delta \theta = 15° \) gewählt.
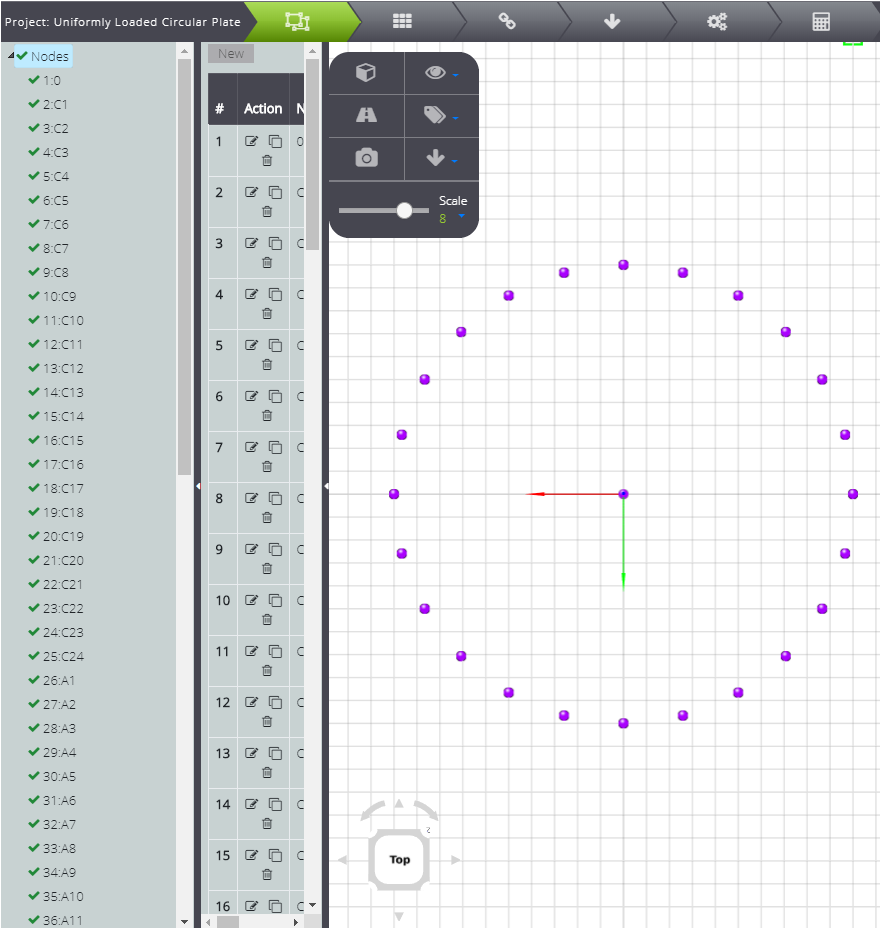
In der folgenden Tabelle können Sie die Koordinaten der Knoten ablesen
| N | X | Y | Z |
|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | 10.00 | 0.00 |
| 3 | 2.59 | 9.66 | 0.00 |
| 4 | 5.00 | 8.66 | 0.00 |
| 5 | 7.07 | 7.07 | 0.00 |
| 6 | 8.66 | 5.00 | 0.00 |
| 7 | 9.66 | 2.59 | 0.00 |
| 8 | 10.00 | 0.00 | 0.00 |
| 9 | 9.66 | -2.59 | 0.00 |
| 10 | 8.66 | -5.00 | 0.00 |
| 11 | 7.07 | -7.07 | 0.00 |
| 12 | 5.00 | -8.66 | 0.00 |
| 13 | 2.59 | -9.66 | 0.00 |
| 14 | 0.00 | -10.00 | 0.00 |
| 15 | -2.59 | -9.66 | 0.00 |
| 16 | -5.00 | -8.66 | 0.00 |
| 17 | -7.07 | -7.07 | 0.00 |
| 18 | -8.66 | -5.00 | 0.00 |
| 19 | -9.66 | -2.59 | 0.00 |
| 20 | -10.00 | 0.00 | 0.00 |
| 21 | -9.66 | 2.59 | 0.00 |
| 22 | -8.66 | 5.00 | 0.00 |
| 23 | -7.07 | 7.07 | 0.00 |
| 24 | -5.00 | 8.66 | 0.00 |
| 25 | -2.59 | 9.66 | 0.00 |
Durch Verbinden der Knoten in der grafischen Oberfläche können Sie alle Shells definieren, aus denen die Platte besteht.
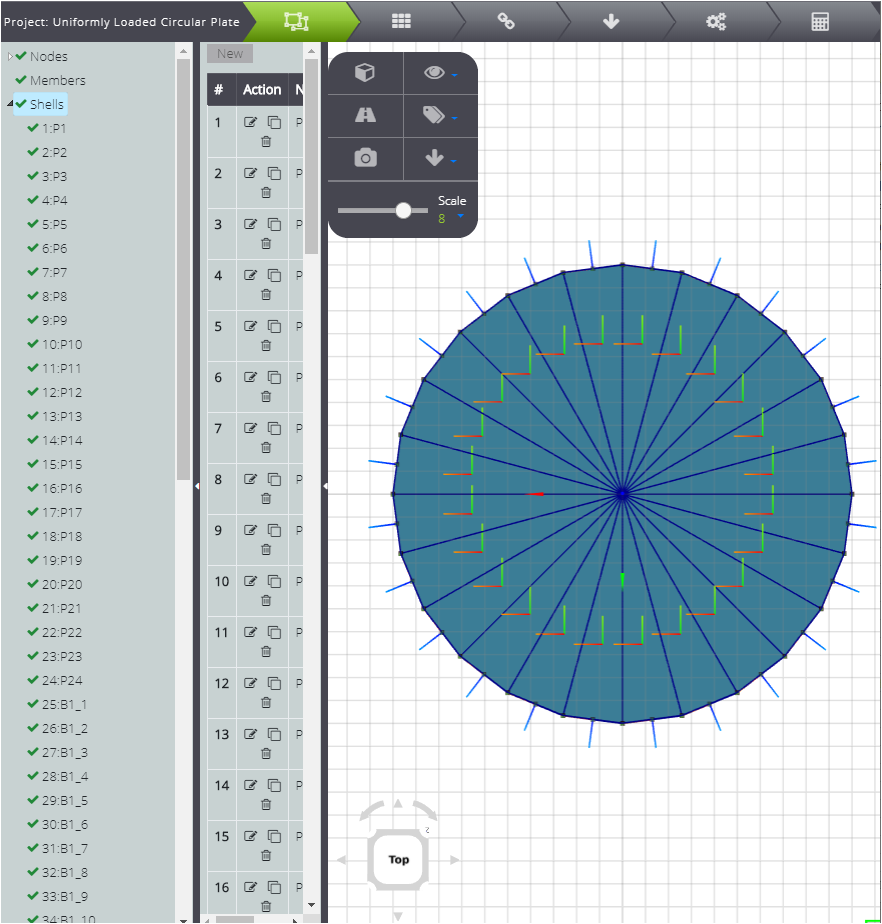
Erstellen Sie nun die eingespannte Kante: Verwenden Sie Clone auf Knoten 2 bis 25 und ändern Sie die z-Koordinate in +1. Erstellen Sie auf die gleiche Weise eine weitere Zeile mit der Koordinate -1.
Erstellen Sie nun Shells: Sie können sich auf der grafischen Oberfläche bewegen und Knoten zusammenführen.
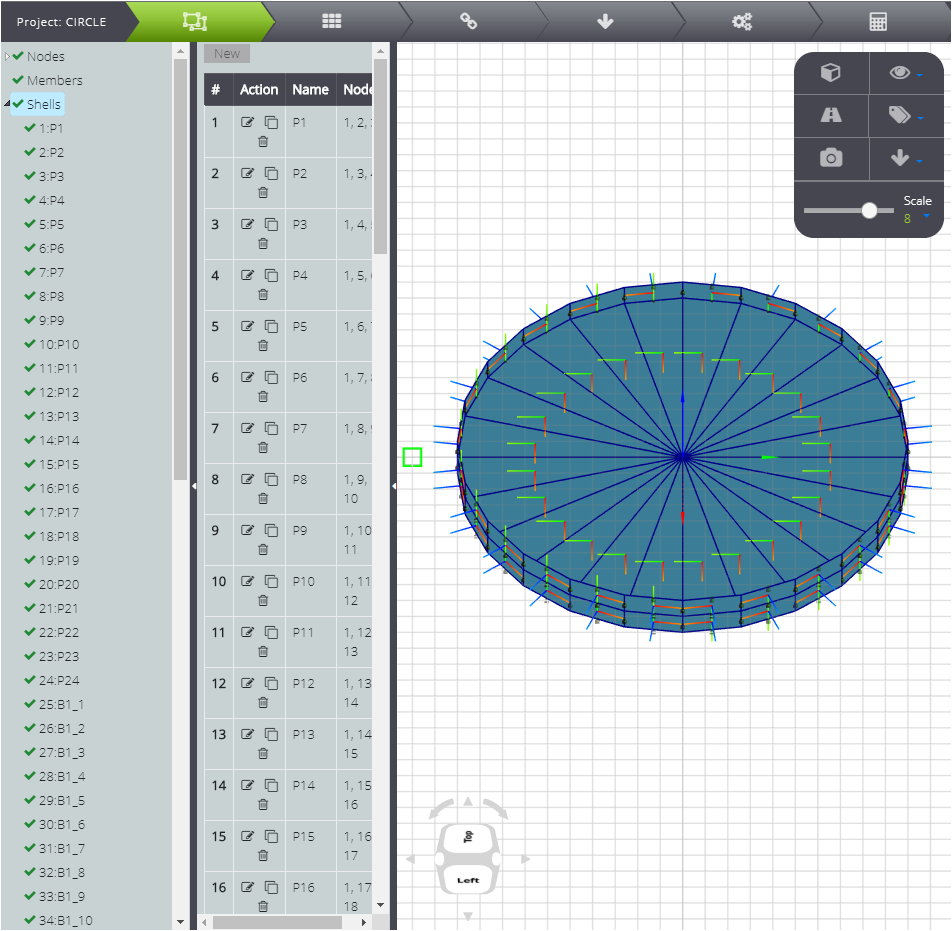
Auf diese Weise haben Sie die Geometrie des Problems definiert. Danach können Sie zu den Eigenschaften gehen.
Eigenschaften
Klicken Sie in der Tab Bar auf PROPERTIES.
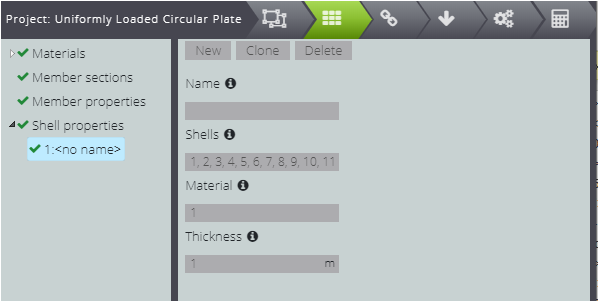
Definieren Sie sofort die Eigenschaften des Materials auf Materials.
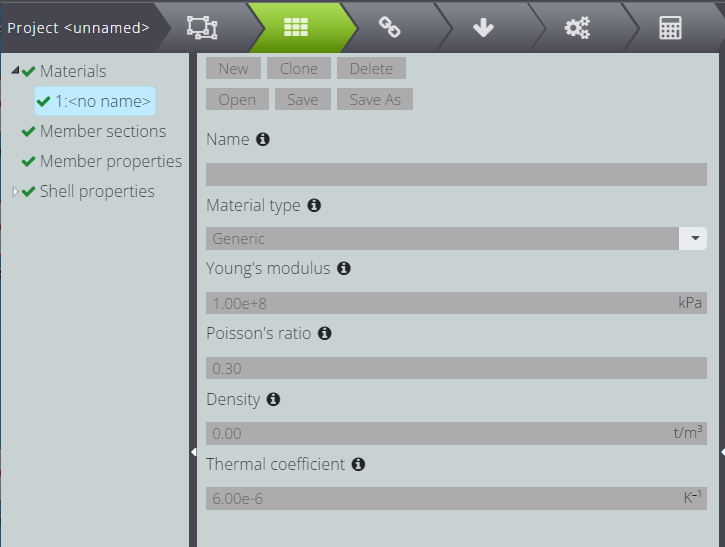
Zum Schluss weisen Sie allen Platten das Material und die Dicke zu: Füllen Sie die Felder aus, wie in der Abbildung unten gezeigt.
Auflager
Die Einspannung der Plattenränder blockiert alle Bewegungen und Drehungen der Schalen, aus denen der Rand besteht.
Öffnen Sie im Entity Tree die Registerkarte CONSTRAINTS , gehen Sie zu Shell Supports und wählen Sie Fixed für alle Freiheitsgrade. Danach brauchen Sie mit Clone nur noch das Feld Shell zu ändern, um eine Beschränkung mit den gleichen Eigenschaften für die anderen Elemente zu erstellen.
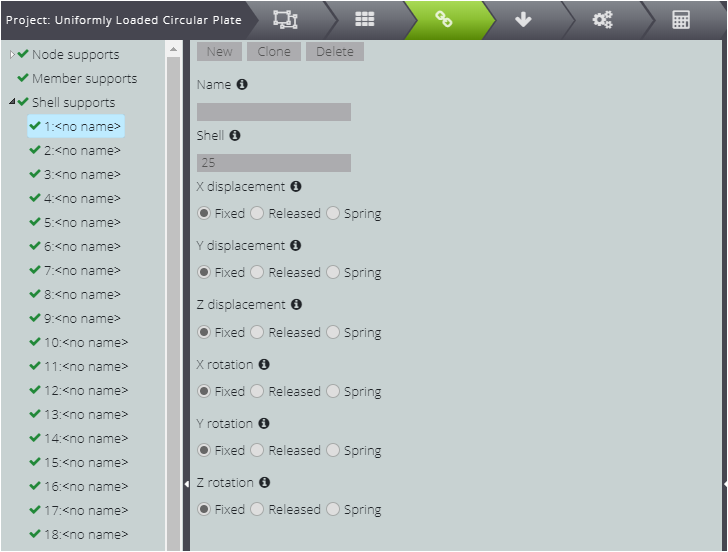
Um das System endlich im Raum zu blockieren, blockieren Sie einen der Knoten: Drücken Sie dazu Node supports im Entity Tree!
Lasten
Gehen Sie nun zu ACTIONS und drücken Sie auf Shell actions, damit Sie die verteilte Last eingeben können.
Füllen Sie für jede Shell, aus der die Platte besteht, das Feld Pressure Z aus, indem Sie -10kPa eintragen.
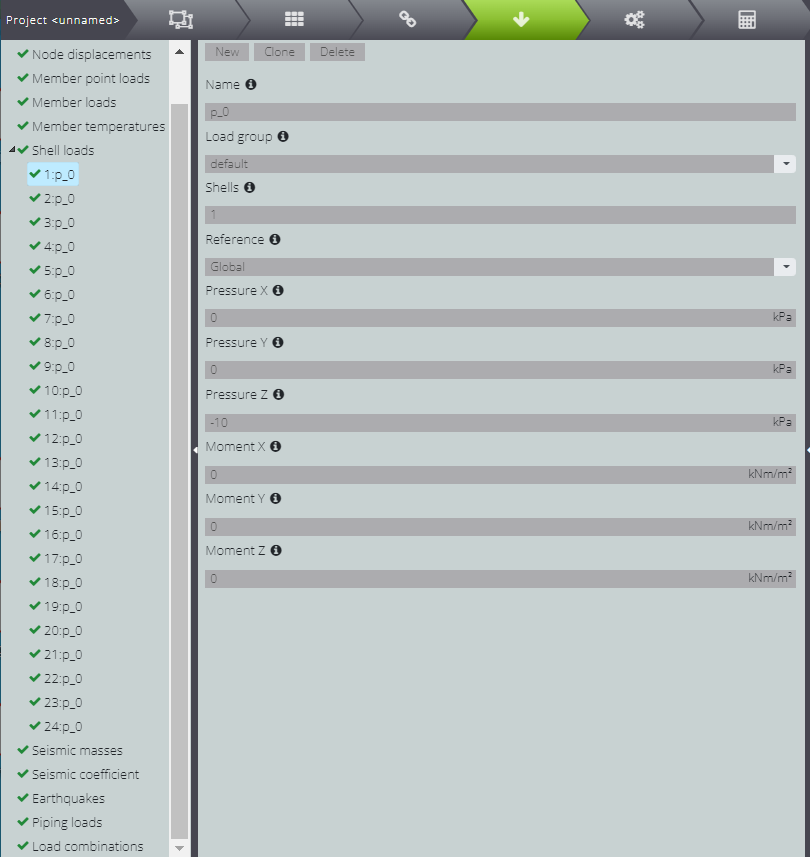
Sie haben alle Eigenschaften des Systems definiert! Gehen Sie auf CALCULATE, um die Analyse zu starten und die Ergebnisse zu lesen.
Für dieses Beispiel gibt es eine analytische Lösung, mit der wir die Ergebnisse von WeStatiX in unserem Verification Manual verglichen haben.
