Auf dieser Seite betrachten wir einen eindimensionalen Träger, der an beiden Enden befestigt ist und einem gleichmäßigen Temperaturanstieg T ausgesetzt wird.
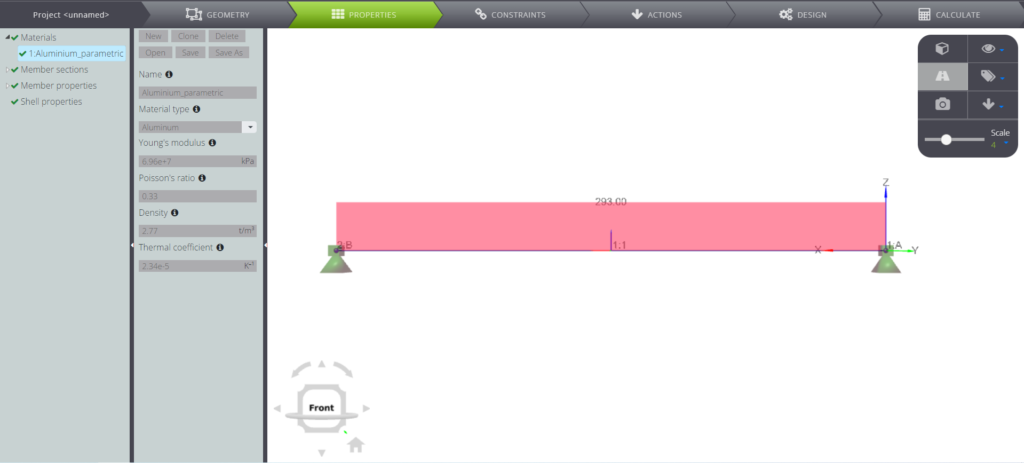
Wenn Sie möchten, können Sie das FE-Modell mit den in der folgenden Tabelle aufgeführten Daten erstellen.
| Elastizitätsmodul | E | 69637000 | kPa |
| Abschnitt | A | 1,00 | \(m^2\) |
| Länge | L | 10,00 | m |
| Koeffizient der thermischen Ausdehnung | \(\alpha\) | 0,0000234 | 1/K |
| Temperaturanstieg | T | 293,00 | K |
Andererseits können Sie das Modell in unsere Tutorials finden, so dass Sie die Berechnung einfach starten können.
Zuerst müssen Sie die analytische Lösung bestimmen: Dazu müssen Sie die axiale Richtung berücksichtigen. 1] Die Dehnung des Balkens durch gleichmäßige Temperaturänderung ist:
\(\epsilon_T=\alpha \cdot T\)
Das Spannungs-/Dehnungsgesetz ist linear, daher ergeben siche die Knotenkräfte
Daher können Sie die analytische Lösung mit den Ergebnissen von WeStatiX vergleichen, wie in der folgenden Tabelle dargestellt.
| BESCHREIBUNG | PARAMETER | EINH. | ANALYTISCHE LÖSUNG | WSX | FEHLER | |
|---|---|---|---|---|---|---|
| Kraft | \(F\) | kN | 477445 | 477445 | 0,00% |
In den Bildern sehen Sie das Diagramm der Normalkraft.
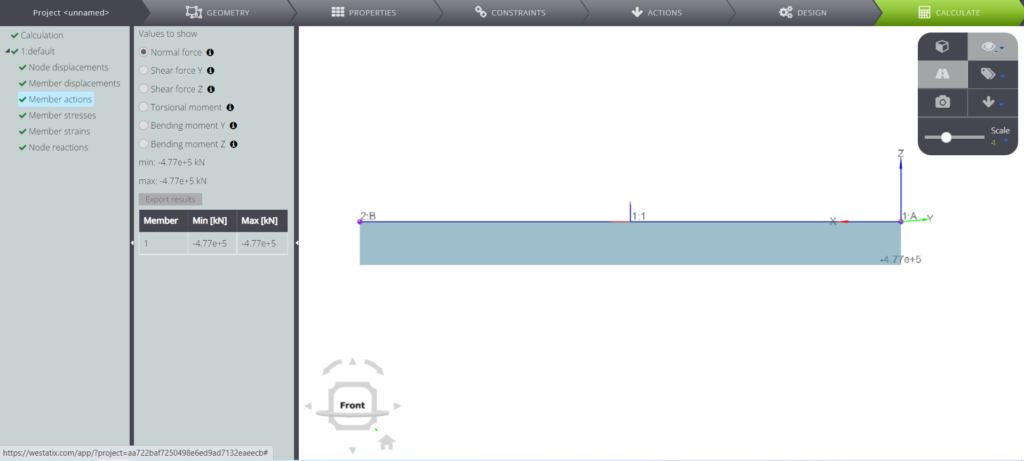
WeStatiX trifft vollständig die Lösung.
[1] DARYL L. LOGAN, A First Course in the Finite Element Method, 4th edition, Thomson
