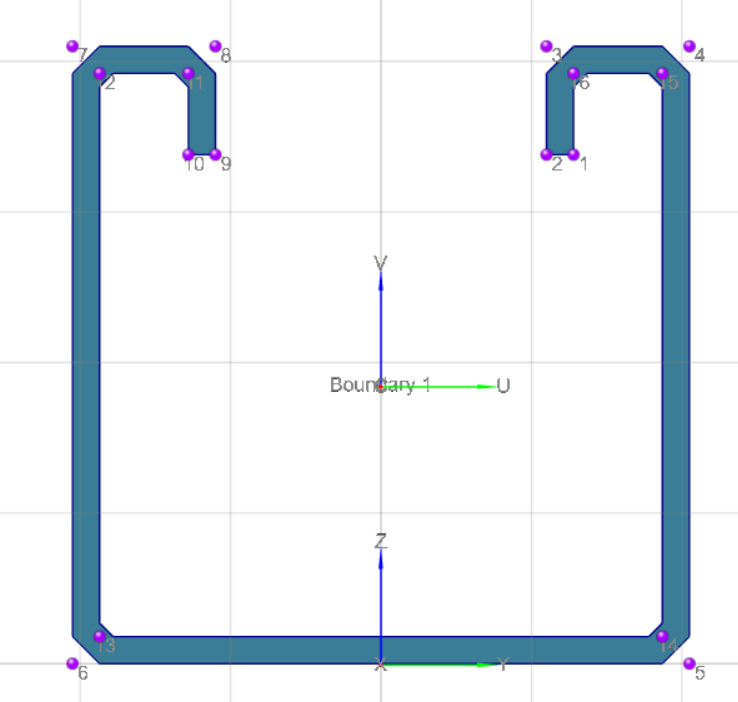
Descrizione della struttura
La struttura in analisi è un sistema di fissaggio muro pavimento.
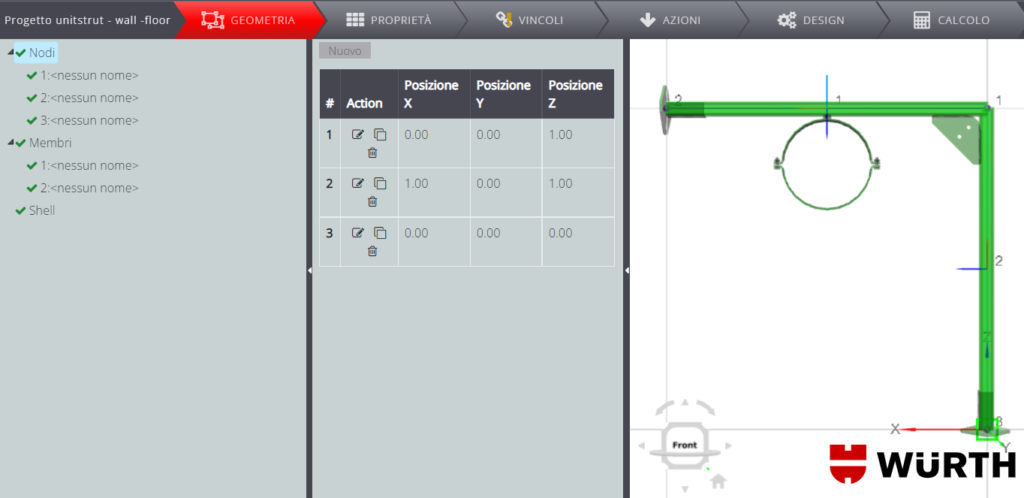
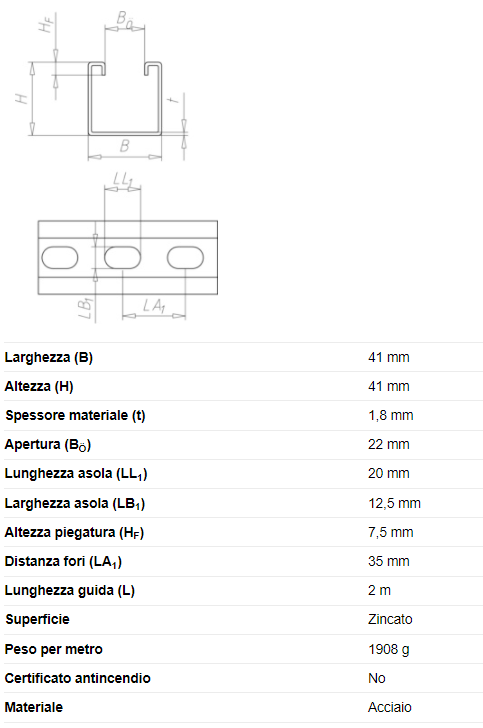
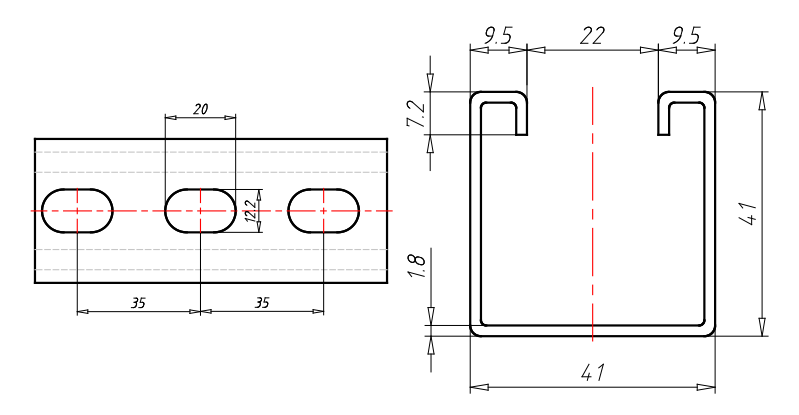
I due membri sono realizzati con profilato di sostegno a C Varifix® 41/41 – C2C (codice articolo 0862001007) e hanno lunghezza unitaria.
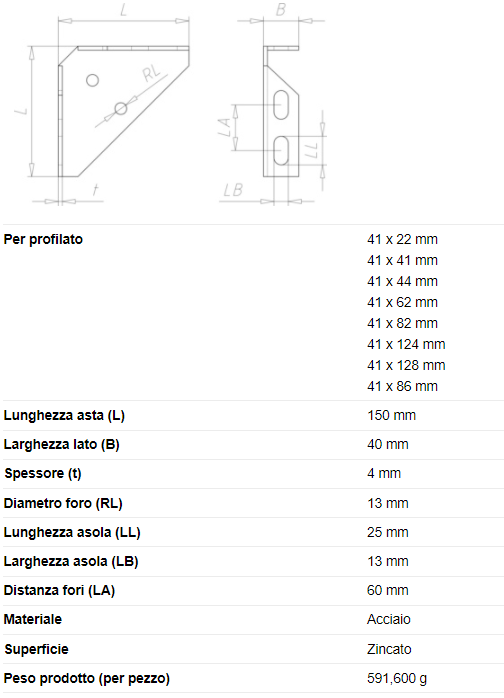
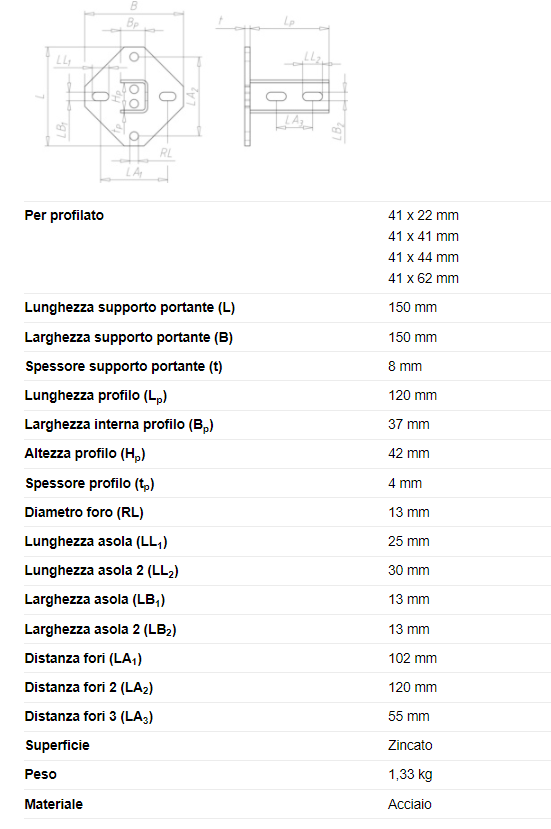
Le connessioni esterne sono staffe femmina per profilato Varifix® 41/41 con piastra a base larga (codice articolo 0862005212) con elementi di fissaggio Plate M12.
La connessione interna è un angolare interno Varifix® con elementi di fissaggio StandardFix M12 (codice articolo 0862005052).
Descrizione dei carichi applicati
La struttura è soggetta al peso proprio degli elementi. Inoltre, un tubo è agganciato al membro orizzontale con un collare TIPP® con diametro di serraggio variabile tra 90 e 102 mm.

Il resto dei parametri utilizzati per definire il carico sono riportati nell’immagine seguente.
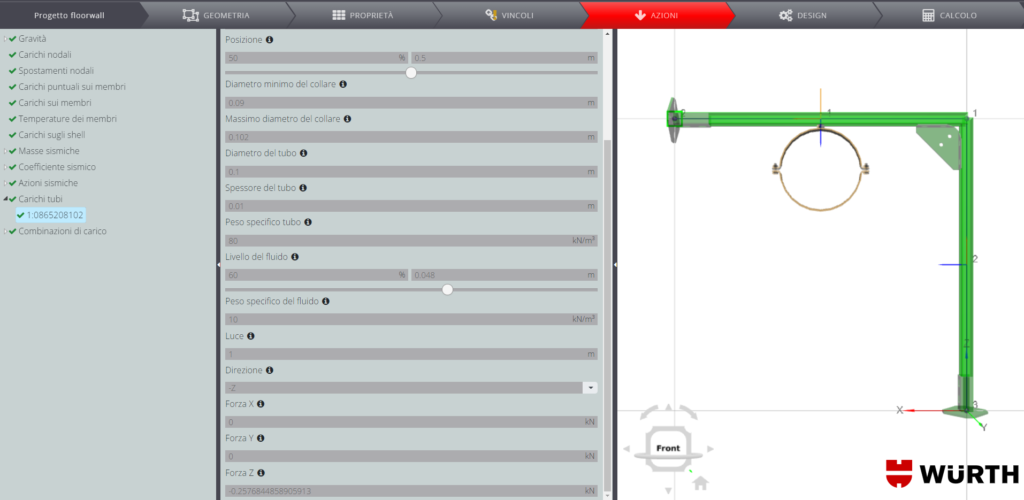
Infine, il sistema, rappresentante un oggetto senza funzione strutturali. è soggetto a azione sismica in direzione X.
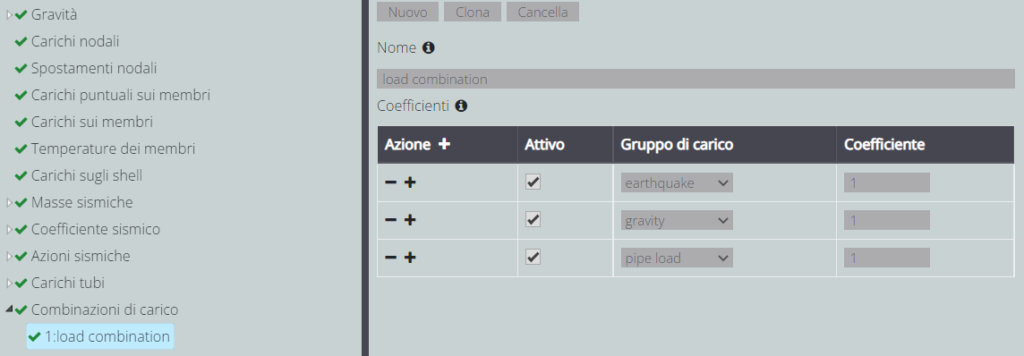
I carichi descritti sono quindi combinati con coefficienti unitari.
Per quanto riguarda la validazione del calcolo delle forze interne, spostamenti e reazioni vincolari con varie condizioni al contorno, fai riferimento al manuale di validazione di WeStatiX. Di seguito puoi trovare invece la validazione di
- azione sismica su elementi senza funzione strutturale;
- verifica dei membri in acciaio;
- verifica delle connessioni in acciaio.
Dettaglio sul calcolo dell’azione sismica
L’azione sismica sul sistema è determinata in conformità a quanto disposto dall’Eurocodice 8. Per calcolarla, viene considerato il peso proprio degli elementi strutturali e la massa concentrata dovuta al tubo.
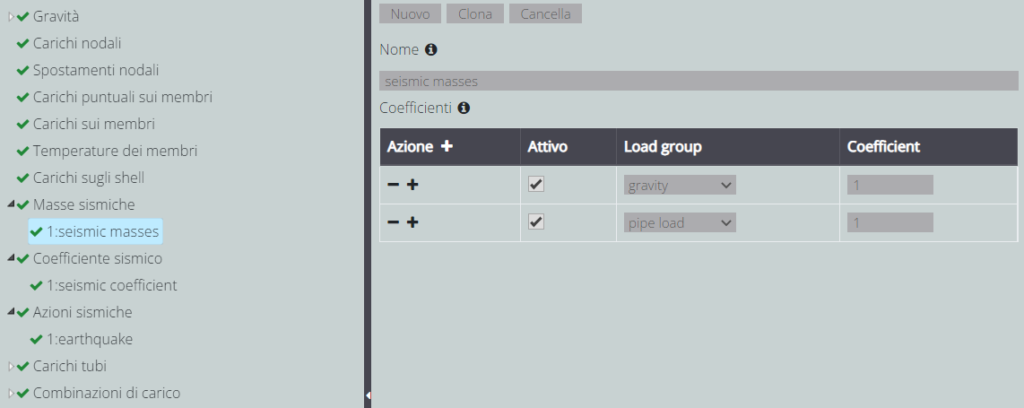
Calcolo del coefficiente sismico
Il coefficiente sismico si calcola come
\( S_a = \alpha \cdot S \cdot \left[\frac{3 \cdot (1 + z / H)}{1 + (1 – T_a / T_1)^2} – 0.5 \right] \)In cui sono dati:
- \( \alpha\): rapporto tra l’accelerazione massima del suolo \(a_g\) sul sottosuolo tipo A da considerare nello stato limite in esame e la gravità \(g\), pari a \(1.0/g\);
- \(S\): coefficiente che tiene conto della categoria del sottosuolo e delle condizioni topografiche, pari a \(1.0\) su suolo di categoria A;
- \(T_a\): il periodo fondamentale di vibrazione dell’elemento non strutturale, pari a \(0.5s\);
- \( z\): l’altezza del centro di gravità dell’elemento non strutturale misurata dal piano di fondazione, pari a \(5m\);
- \( H\): l’altezza dell’edificio misurata dal piano di fondazione, pari a \(10m\).
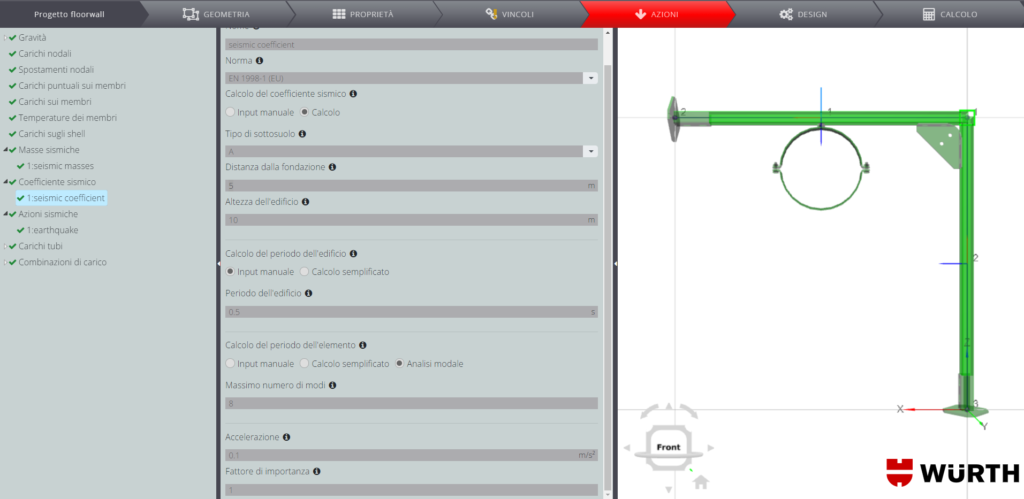
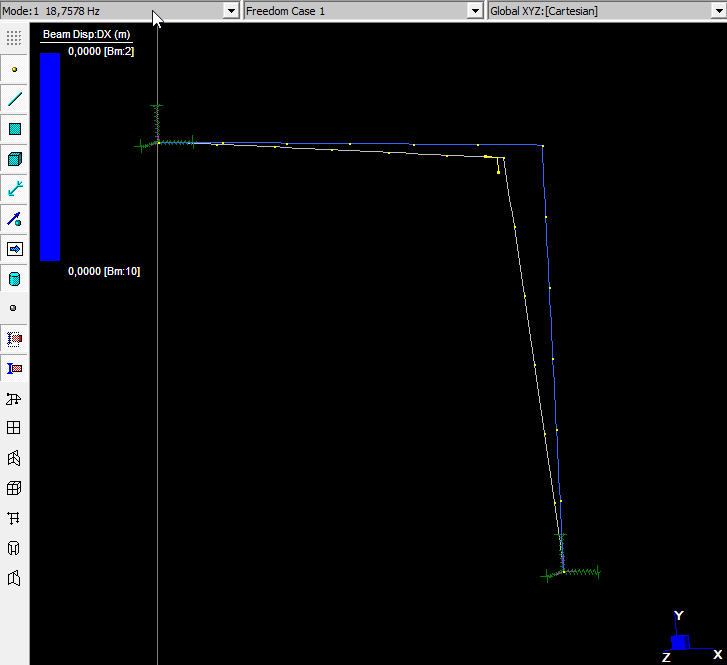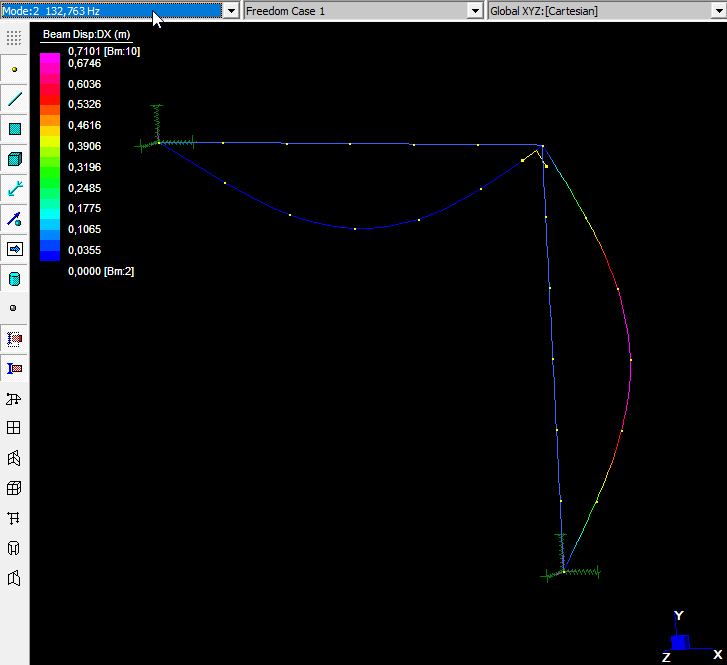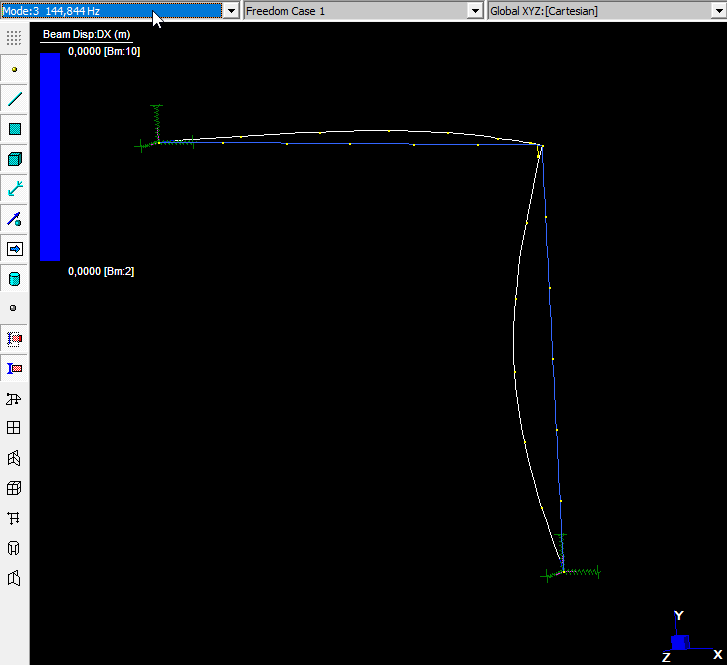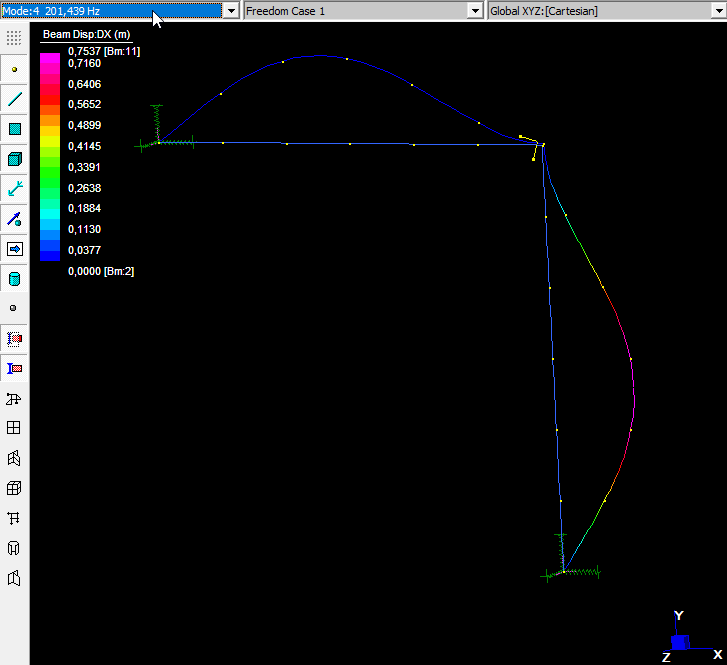
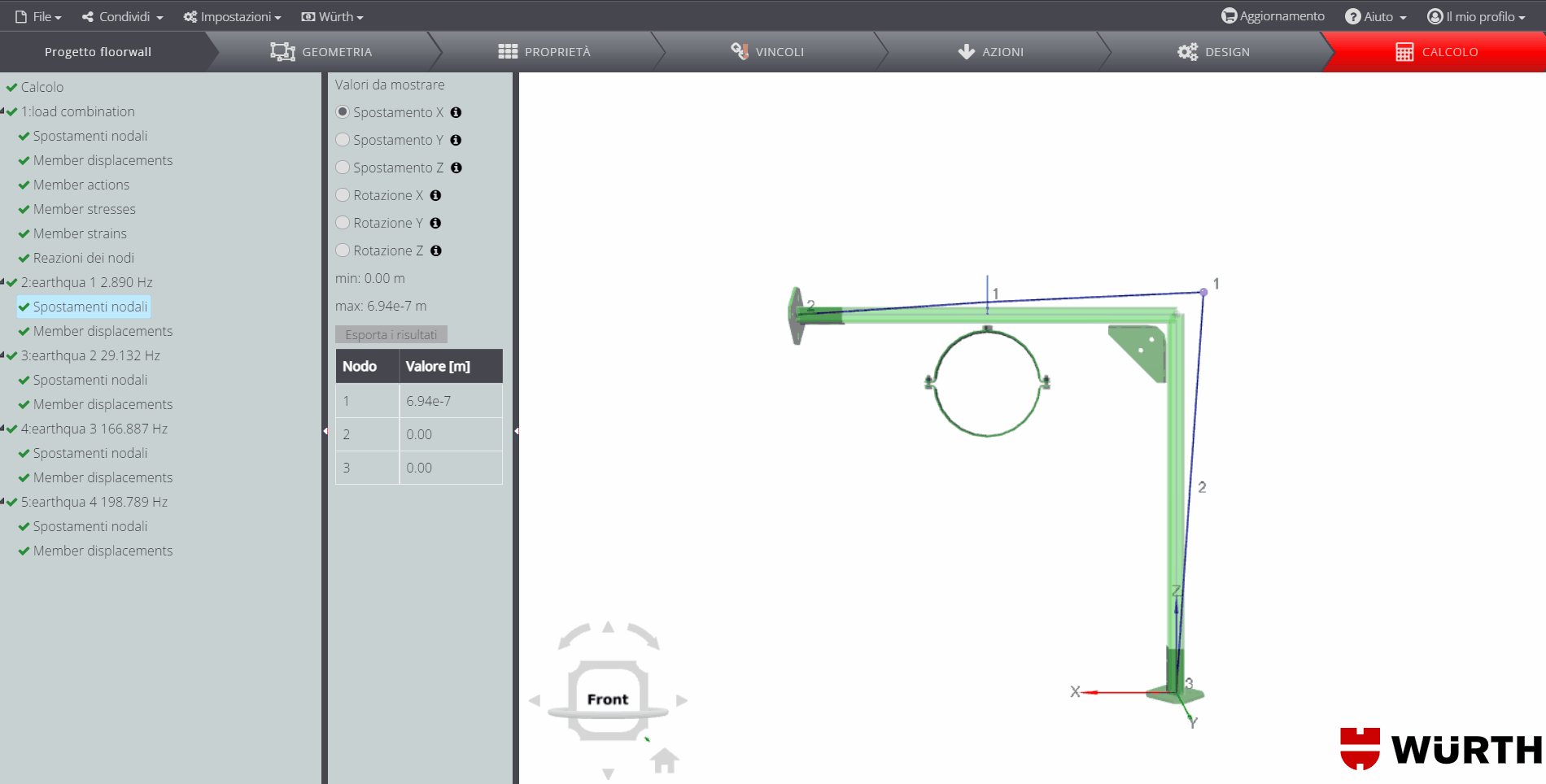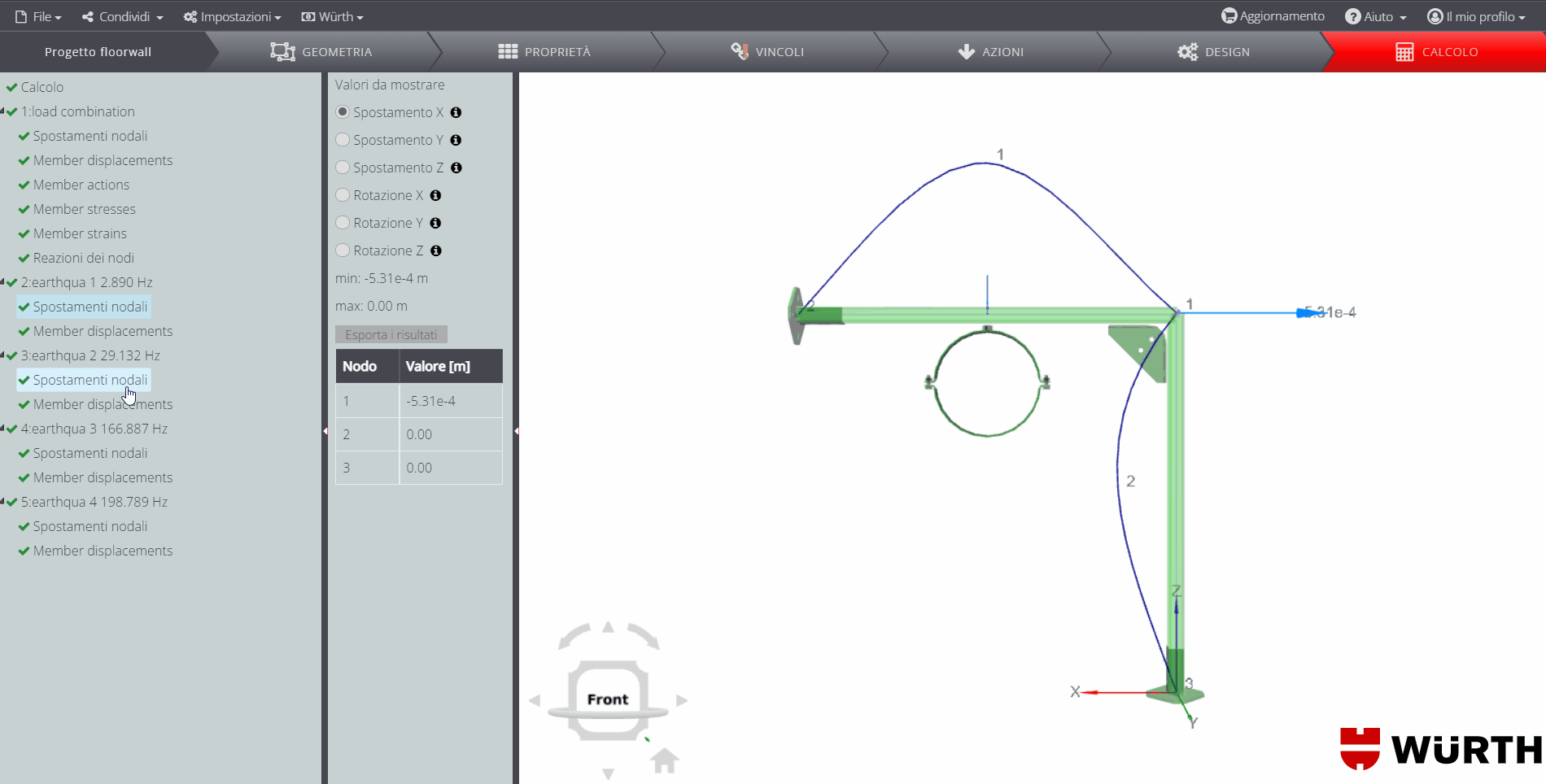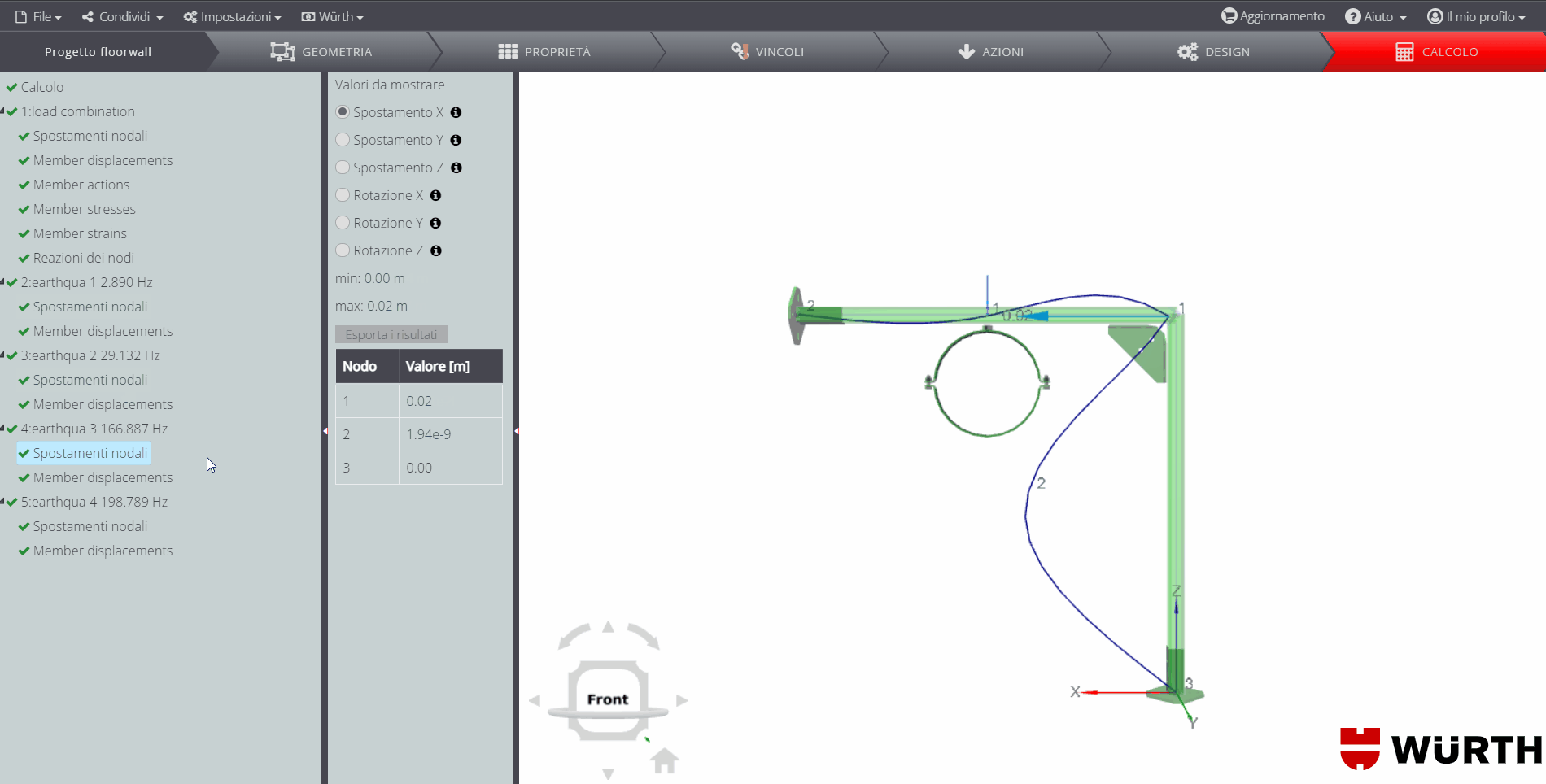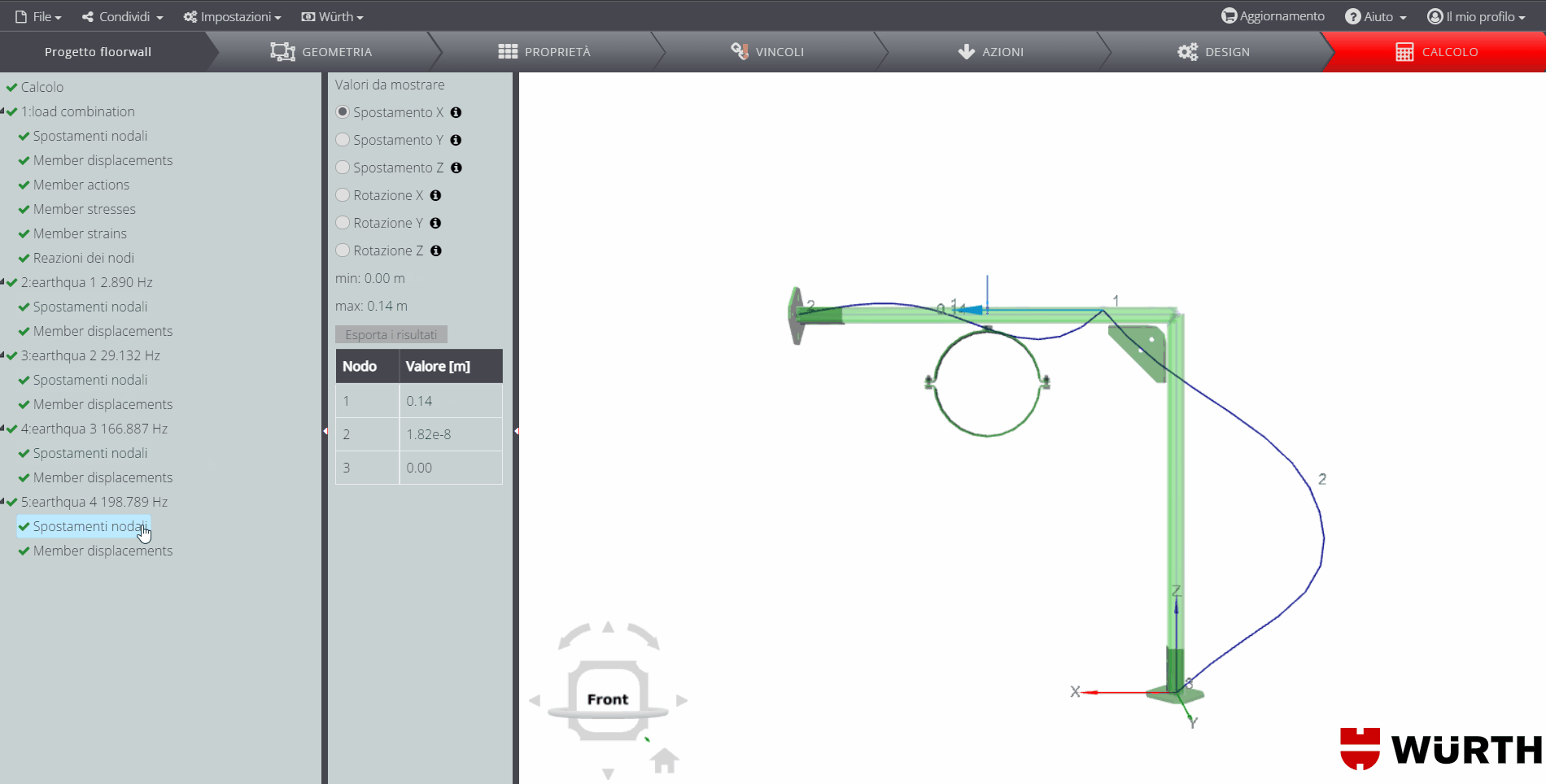
\(T_1\) è il periodo fondamentale di vibrazione della struttura nella direzione considerata e viene calcolato tramite analisi modale, impostando il massimo numero di modi da determinare pari a 15. Tra questi, 4 convergono.
L’ultimo, con frequenza pari a \(198.789Hz\), ha la maggiore massa partecipante nella direzione del sisma: conseguentemente il periodo \(T_1 = 0.00503s\)
Il coefficiente sismico è quindi \(0.102 * (4.5 / (1 + (1 – 0.00503 / 0.5) ** 2) – 0.5) = 0.18\)
cALCOLO DELLE FORZE STATICHE EQUIVALENTI
Secondo il paragrafo 4.3.5.2 della EN1998
\(F_a = S_a \cdot W_a \cdot \gamma_a / q_a\)in cui
- \(\gamma_a\) è il coefficiente di importanza, posto uguale a 1.00
- \(q_a\) è il fattore di struttura, calcolato in base al tipo di elemento secondo la tabella 4.4, paragrafo 4.3.5.4. Si sceglie il tipo “Parapetti”, che porta a un fattore di struttura pari a 1.0 a favore di sicurezza.
- \(S_a\) è stato calcolato al paragrafo precedente ed è pari a 0.18.
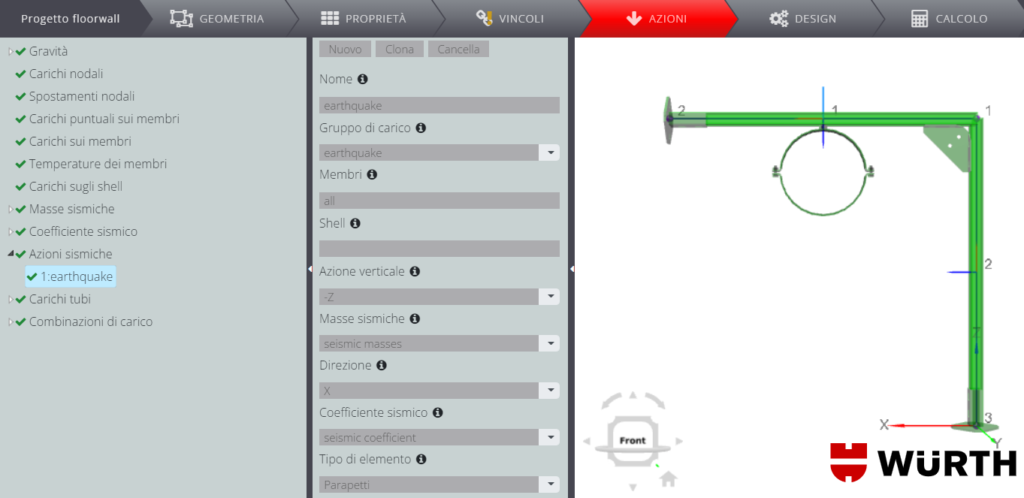
Dato che le masse che sono affette dall’azione sismica sono i membri e il peso proprio, l’azione stessa può essere ricondotta ai seguenti carichi statici equivalenti in direzione X:
- carico distribuito uniforme su entrambi i membri (\( W_a=0.0196 \)) pari a \(0.00353 kN/m\)
- carico puntuale applicato in corrispondenza del tubo (\(W_a=0.258\)) pari a \(0.0464kN\)
I carichi sopra citati sono definiti in un nuovo gruppo di carico “equivalent”. Si comparano quindi i risultati ottenuti con questo gruppo di carico e con il solo terremoto: i due sono equivalenti.
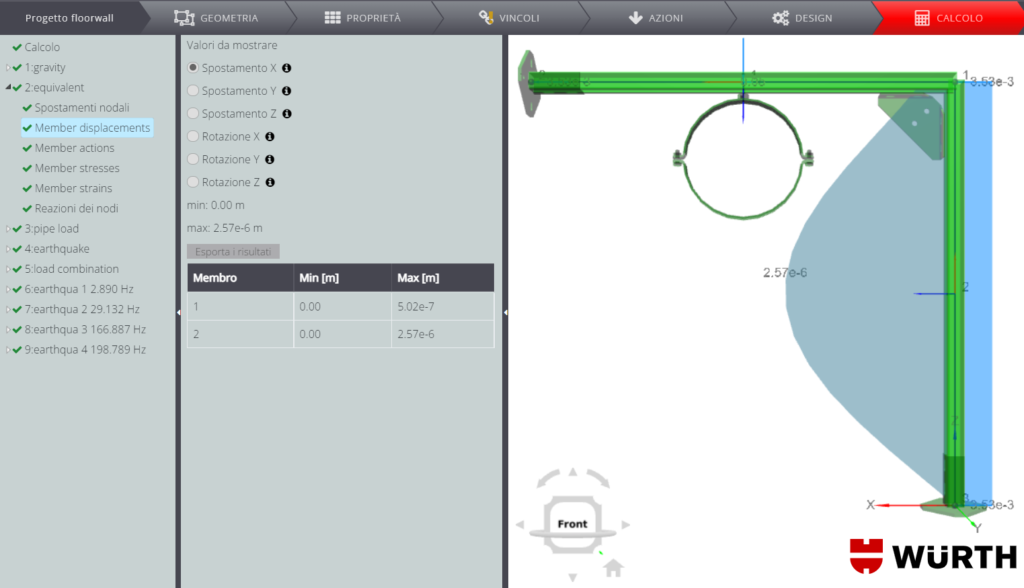
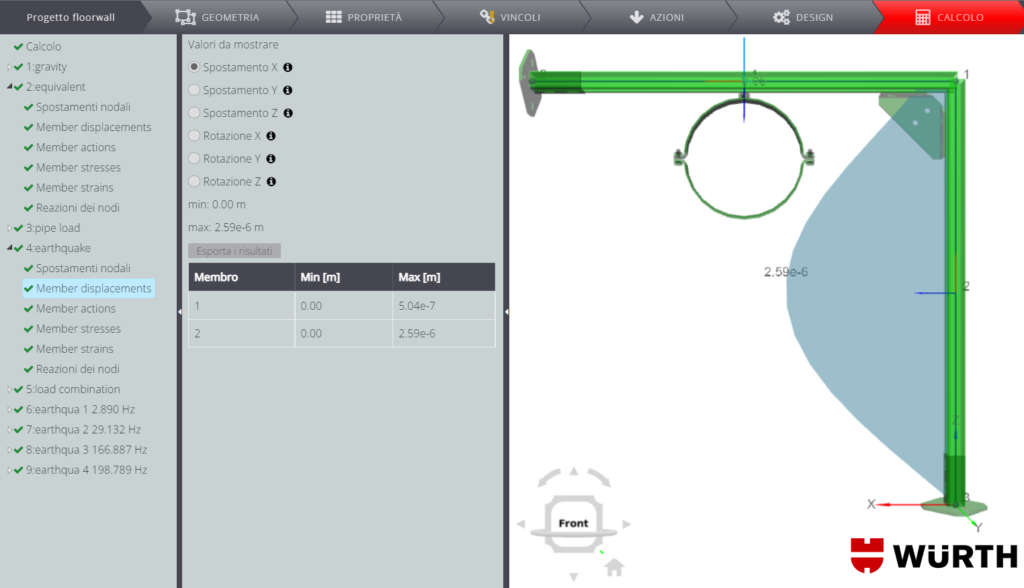
Gli effetti dell’azione sismica sono quindi calcolati correttamente.
Risultati
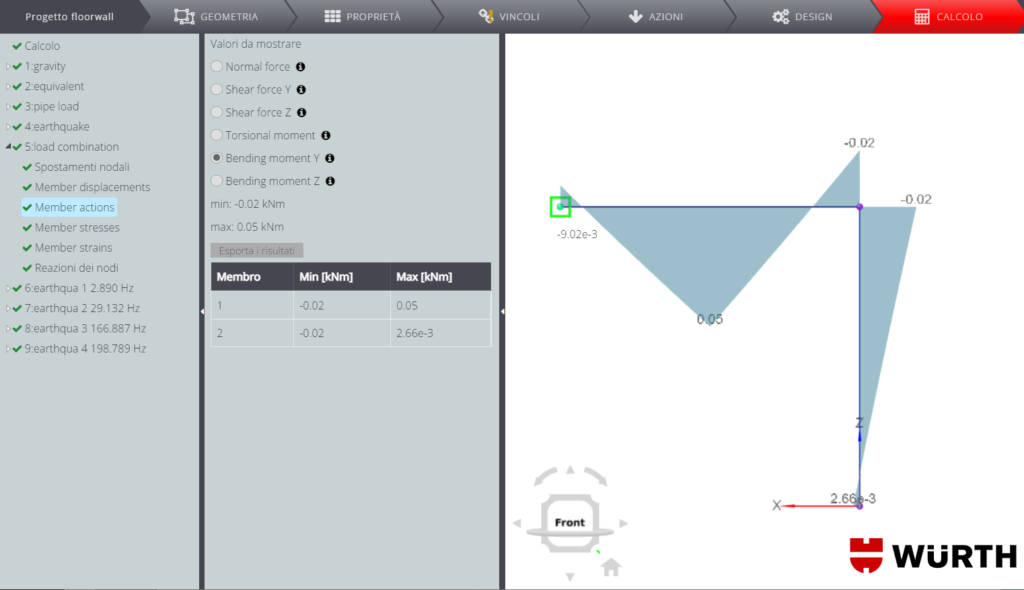
Si riportano di seguito i diagrammi delle forze interne. Ricorda che puoi trovare tanti altri esempi di validazione dei risultati di spostamenti e forze interne nel manuale di validazione generale dell’applicazione. Di seguito troverai invece il dettaglio sulla validazione dei risultati della verifica delle connessioni interne ed esterne e della verifica del membro in acciaio.
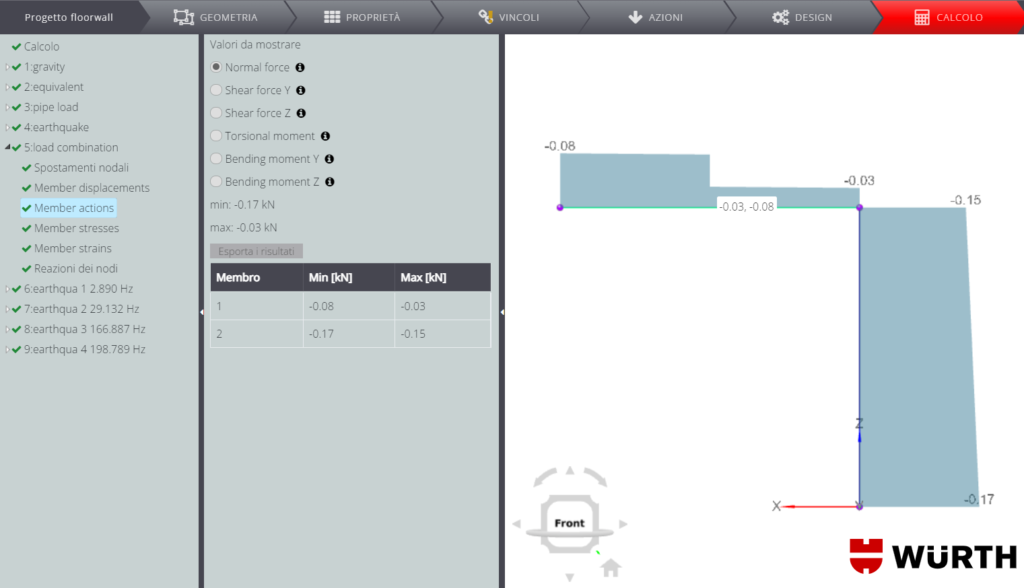
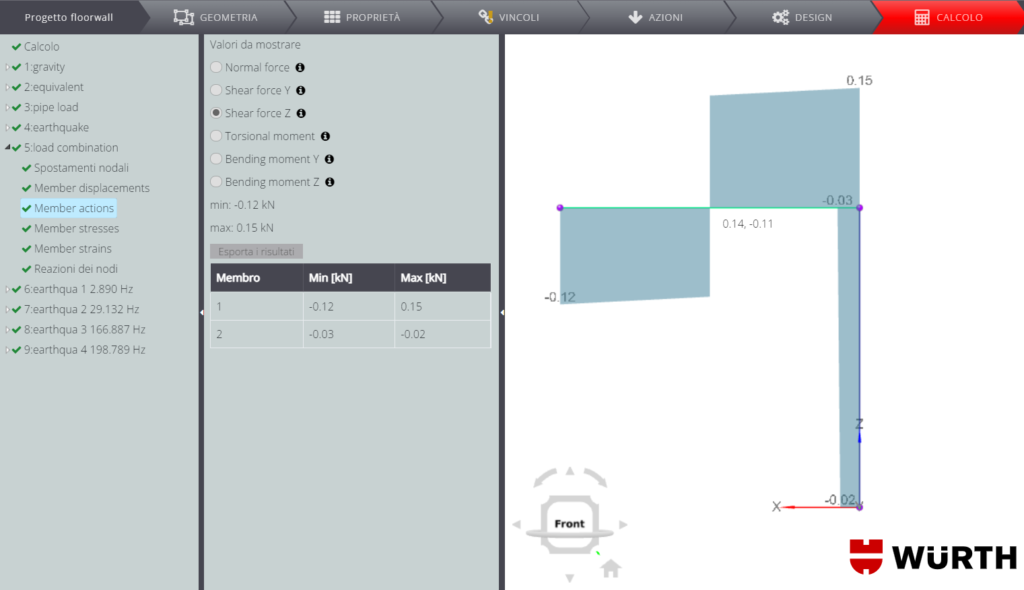
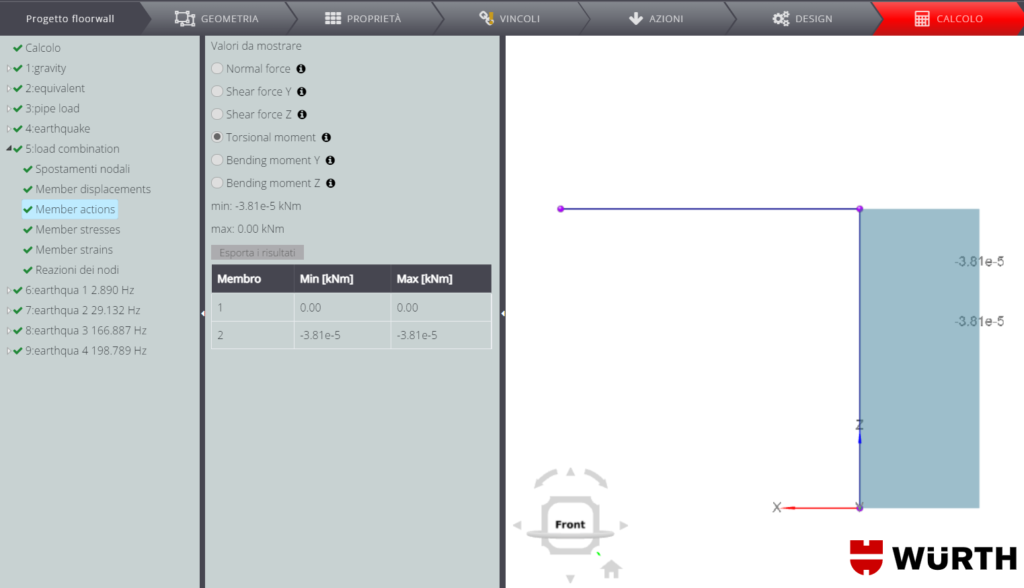
Verifica delle connessioni INTERNE ED ESTERNE
La resistenza delle connessioni nelle varie direzioni è stata calcolata numericamente o sperimentalmente. Nelle tabelle seguenti si calcolano i rapporti di utilizzo parziali sulle connessioni dividendo l’azione agente per la resistenza, e si compara il risultato con quello ottenuto con WeStatiX. Nota che i risultati parziali riguardo ai rapporti di utilizzo sono consultabili nella relazione di calcolo.
| hinge 0862005052 | action | resistance | ratio | ratio wsx |
|---|---|---|---|---|
| Sforzo normale | 0.0283 | 3.9800 | 0.0071 | 0.0071 |
| Taglio y | 0.0004 | 3.9800 | 0.0001 | 0.0001 |
| Taglio z | 0.1535 | 3.9800 | 0.0386 | 0.0386 |
| Momento y | 0.0239 | 0.5100 | 0.0469 | 0.0469 |
| fixity 0862005212 | action | resistance | ratio | ratio wsx |
|---|---|---|---|---|
| Sforzo normale | 0.0785 | 2.1200 | 0.0370 | 0.0370 |
| Taglio y | 0.0000 | 8.3000 | 0.0000 | 0.0000 |
| Taglio z | 0.1238 | 8.3000 | 0.0149 | 0.0149 |
| Momento y | 0.0090 | 0.5935 | 0.0152 | 0.0152 |
| Momento z | 0.0002 | 0.5935 | 0.0003 | 0.0003 |
A favore di sicurezza, i parziali vengono sommati linearmente per determinare il rapporto di utilizzo totale, mostrato nell’applicazione: essendo il rapporto totale inferiore a 1.00, tutte le connessioni interne sono verificate.
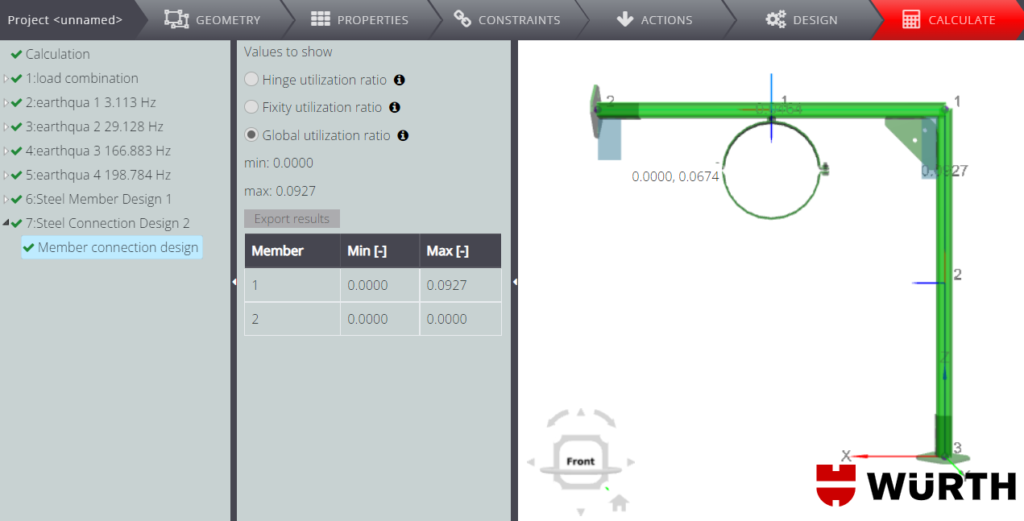
Verifica dei membri in acciaio
La verifica dei membri in acciaio è impostata per il membro orizzontale e la prima combinazione di carico, in conformità alle disposizione dell’EN1993.

Classificazione
Il limite di snervamento del materiale che costituisce la sezione è \(f_y = 280000kPa\), quindi il coefficiente \(\epsilon=\sqrt{235/f_y} = 0.916\).
Considerando a favore di sicurezza la sezione completamente compressa, si classificano l’anima e la flangia
| part | inner/outstand | c | t | c/t | classE | |
|---|---|---|---|---|---|---|
| flangia | esterna | 35.6 | 1.8 | 19.77 | > 14 \(\epsilon\) = 12.83 | 4 |
| anima | interna | 35.6 | 1.8 | 19.77 | < 33 \(\epsilon\) = 30.23 | 1 |
Dove la sezione è soggetta a compressione pura, questa ricade in classe 4 e la lunghezza delle flange deve essere ridotta per considerare gli effetti dell’instabilità locale. Trascurando gli irrigidimenti a favore di sicurezza e considerando la tabella riportata in EN1993.1.5.
| Lunghezza della flangia | \(b\) | 35.6 | mm |
| Spessore della flangia | \(t\) | 1.8 | mm |
| \(\epsilon\) | 0.916125381 | – | |
| Coefficiente di imbozzamento | \(k_{\sigma}\) | 0.43 | – |
| Snellezza relativa | \(\bar{\lambda}_p\) | 1.163327285 | – |
| Rapporto tensioni | \(\psi\) | 1 | – |
| Fattore di riduzione | \(\rho\) | 0.697041391 | – |
| Lunghezza effettiva | \(b_{eff}\) | 24.81467353 | mm |
La sezione effettiva ha quindi le seguenti proprietà
| Area | 1.65E-04 | \(m^2\) |
| Momento d’inerzia U | 1.28E-08 | \(m^3\) |
| Momento d’inerzia V | 4.53E-08 | \(m^3\) |
| Centroide Y | 0.00 | \(m\) |
| Centroide Z | 8.69E-03 | \(m\) |
Nella parte cetrale del membro invece l’asse neutro è spostato a causa della flessione: la lunghezza compressa delle flange è quindi tale per cui la sezione ricade in classe 3. In questa zona vengono quindi considerate le proprietà elastiche della sezione intera.
Verifica di resistenza
Di seguito è riportata la verifica del punto centrale del membro, dove le forze interne sono più alte: esse sono riepilogate nella seguente tabella.
| sforzo normale \(N\) | -0.077 | kN |
| taglio z \(V_z\) | 0.144 | kN |
| momento y \(M_y\) | 0.05 | kNm |
Le proprietà geometriche della sezione sono le seguenti:
| Area | 2.5479E-04 | \(m^2\) |
| Momento d’inerzia U | 5.8169E-08 | \(m^3\) |
| Momento d’inerzia V | 7.1281E-08 | \(m^3\) |
| Centroide Y | 0.00 | \(m\) |
| Centroide Z | 1.8480E-02 | \(m\) |
| Modulo elastico U | 2.5830E-06 | \(m^2\) |
| Modulo elastico V | 3.4771E-06 | \(m^2\) |
| Costante torsionale | 2.7663E-10 | \(m^4\) |
| Costante di warping | 3.1992E-11 | \(m^6\) |
| Centro di taglio U | 0.00 | \(m\) |
| Centro di taglio V | -4.0852E-02 | \(m\) |
| Momento statico U | 1.7535E-06 | \(m^3\) |
| Momento statico V | 2.0196E-06 | \(m^3\) |
Il vertice più sollecitato nella sezione sopra raffigurata è il numero 4 con coordinate (20.5, 22.6) nel sistema di riferimento principale U, V. Su di esso, le tensioni sono
\(\sigma_N = N / A_{eff} = 301kPa\);
\(\sigma_{M_y} = M_y \cdot 0.0226 / J_{U_{eff}} = 19519kPa\);
\(\tau_{V_z} = \frac{V_z \cdot S_u}{J_u \cdot t} = \frac{0.144 \cdot (22.5 \cdot 19.74) / 1^9}{1.28E-08 \cdot 0.0018} = 207kPa \)Sommando questi con il criterio di von Mises si ottiene
\( \sigma_{eq} = 19450kPa\)
Comparato con il risultato ottenuto con WeStatiX
Il risultato è quindi accettabile.
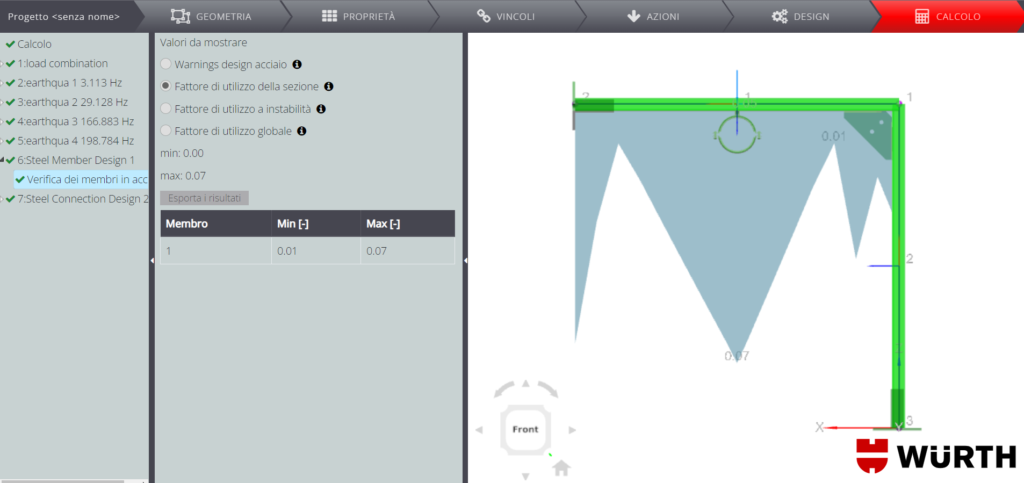
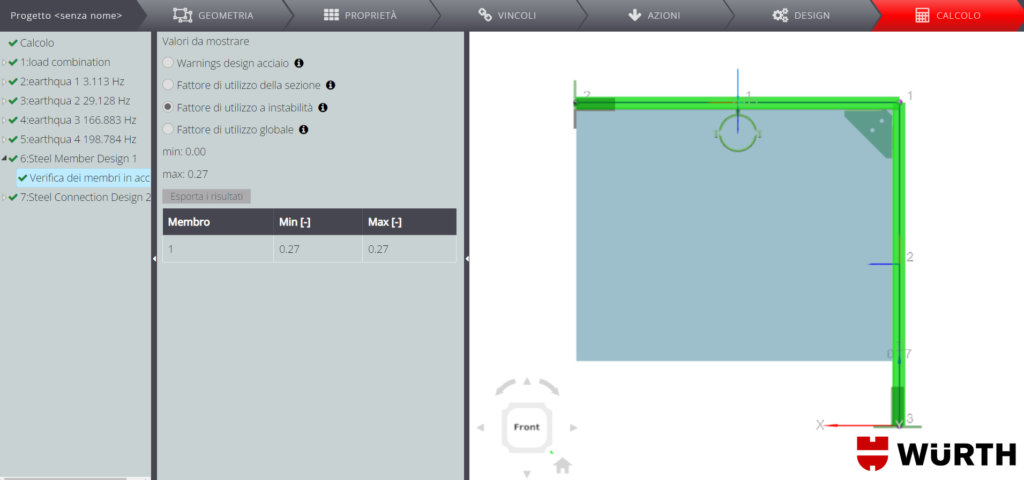
Nelle immagini soprastanti puoi vedere il rapporto di utilizzo per la verifica di resistenza e a instabilità. Essendo questo rapporto inferiore a 1.00 in tutti i punti del membro, allora la verifica è soddisfatta.
Nota che anche in questo caso puoi consultare i parziali dei risultati nella relazione di calcolo.